実戦！ミニロトチャレンジ【第1099回】🎃2020/10/20抽せん

外れの呼吸！shirono-j🤠です。

ボクの基本的な考え方として、

「４等の当せん率を上げる事が１等当選に近づく最短の道」というのがあります。

野球でいえば、「ヒットの延長がホームランである」というのと一緒です。

先週から、その最終形と考えているロジックの「型」を採用しています。

効果を測るには、他のパターンの誘惑に負けずに長期間貫き通す必要があります。

誘惑に負けない自信はある。

これまでしてきた失敗がきっと血肉になっている。

問題はどこで見極めるか、ダメならどこで見切るか。🧐

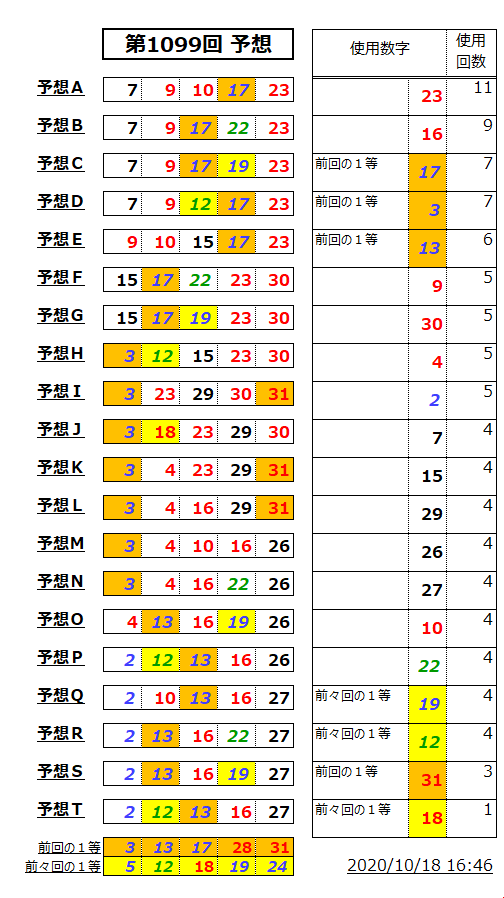
ミニロト予想

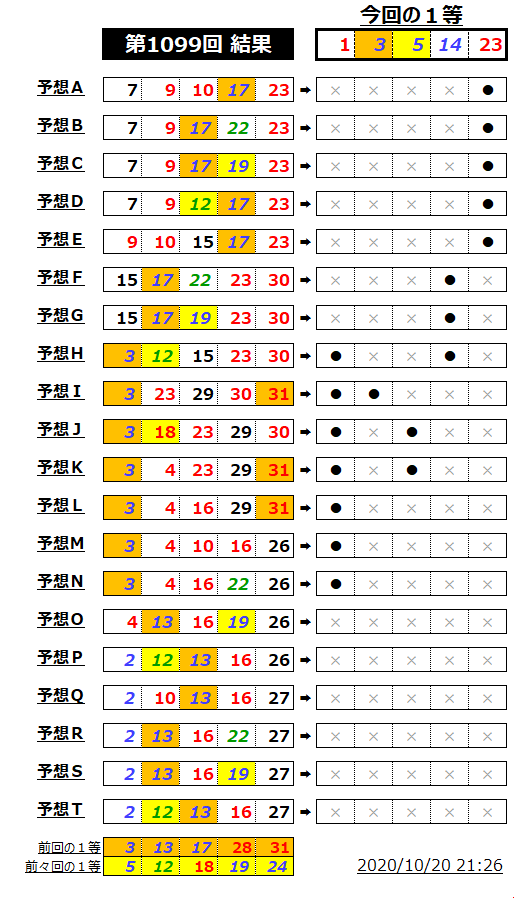
ミニロト反省

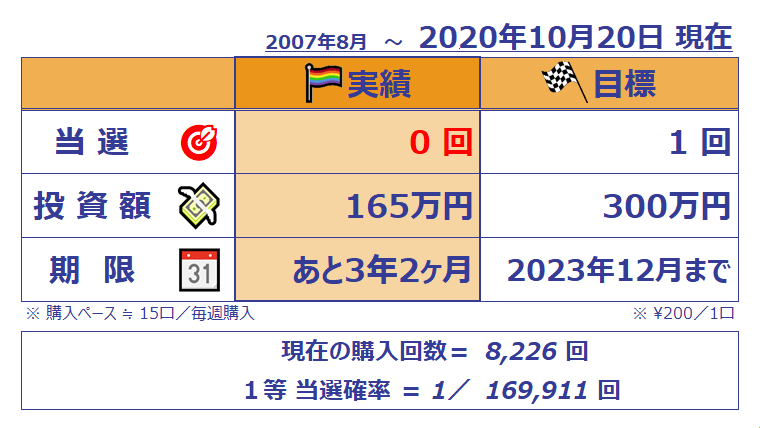
ミニロト実績

今週のひと言

愚かに還って、ただひたすら己が仕事に専念すべし！

「愚かに還って」とは、この場合、純粋だった若い頃の気持ちに戻ってってことね。

「愚かに帰って」と書いちゃうと、❝大人としてのふさわしくない行為を非難めかして言う言葉。❞になるらしい。

けれど、いつまでも始めた頃の「楽しい」だけという訳にはいかないな。

やっぱ当てたい。🤠

#修身教授禄①P22

❝全ての人間の生活は、ある意味では皆みじめなり。自分のみと思う事なかれ。表を見、裏を見、愚かに還ってひたすら己が仕事に専念すべし❞

🤠
どれだけ幸せでも、所詮ひとは無い物をねだって悩むもの
よく見ればみんな同じ
自分の成長に集中してればいいhttps://t.co/9x9y20j2gH pic.twitter.com/zoVKQ1uWuz

— shirono-j (@shironojpn) October 14, 2020

スポンサーリンク

直近50回の発生データ

直近50回分のデータを羅列。毎週更新して最新を保ちます。

「前回の１等」や「前々回の１等」の出現状況も『色』で表現してある。

※
パターン色について興味のある方はコチラの説明をご覧ください　→　直近２回での出現し易さ（色のパターン）

統計データ掲示板

ミニロトのために統計の勉強中。少しでも１等当せんへ近づけないか、何とか攻略できないものかと必死です。

勉強した知恵を利用して整理した、最新のデータをここに公開。アホかと思われるかもですが、勝てば官軍。正義が勝つのではなく、勝った者が正義なのだ！

がんばって、最後に勝つ！🤠

度数分布表；全31数字×桁別

全31数字の発生頻度を「桁別」でカウントして整理した集計表。

「計」と「発生率」の列では、

• 平均以上値＝ピンク枠で太字
• 最大値＝青枠で太字
• 最小値＝緑枠で細字
• その他＝白枠で細字

となってます。

出現度数；ヒストグラム

出目頻度のヒストグラム（度数分布）を「桁別」で書き出したもの。

※
ピンクの部分が「桁ごと」の度数を表し、グレーの部分は全体を表します。

第１回から現在までの「全抽せんデータ」で分析しています。

度数分布に関してのボク🧐の理解程度はコチラを参照ください。→ クリック↗

右側の図は、最近勉強した「箱ひげ図」です。

移動平均；折れグラフ

出目頻度の移動平均を「桁別」にとってグラフ化したもの。

過去201回分の移動平均を連続させた 折れ線グラフにしています。

1. 最新～ n=8レンジ（８回移動平均）
2. 最新～ n=17レンジ（17回移動平均）
3. 最新～ n=32レンジ（32回移動平均）

の３種類を、ひとつのグラフに重ね合わせている感じです。

移動平均に関してのボク🧐の理解程度はコチラを参照ください。→ クリック↗