ミニロト歴19年目。一週たりとも休まずに予想購入を継続しています。
まだ一度も当てていない予想方法だけど、16年目の集大成として整理してみた。ひと言でいえば、「週替わりで六つのルールを決めて予想する」といった方法だ。当ててもないのに偉そうに予想方法を公開するのは抵抗があったが、「当たったら即で自慢げに公開するよりかは好い」と思ってやってみた。
全ては「いずれ当たる」ことを前提に行動している。
予想作業標準
日々 考案と改良を繰り返して、最近だいぶん手法や考え方が安定してきた。作業の手順に変更や追加が少なくなり、ヒット率も徐々に安定してきたと思う。そろそろ、標準として文書化しても良いと考えた。
予想作業の手順は大きく次の段階からなる。
- コンセプトを決める
- 主軸を固める
- 仕上げ
- 完了
順に整理していこう。
コンセプトを決める(手順①)
まず最初に、予想のコンセプトを決める。
一回の抽せんに対し「20口」の購入するが、その予想構成を決める作業となる。具体的には、これまで観察してきた発生パターン×6項目をひとつひとつ想定していく作業であり、そこまでの結果によって毎週違ってくる。
コンセプトを決める為に使用するパターン6項目とは以下の特性から分析したもの。
1) 直近2回での出現し易さ
2) 直近7回での出現特性
3)「桁」ごとに見出す安定性
4)「week数」から見出す安定性
5) week出現回数の平均との関係
6) 出現率から見出す特徴
1) 直近2回での出現し易さ(色のパターン)
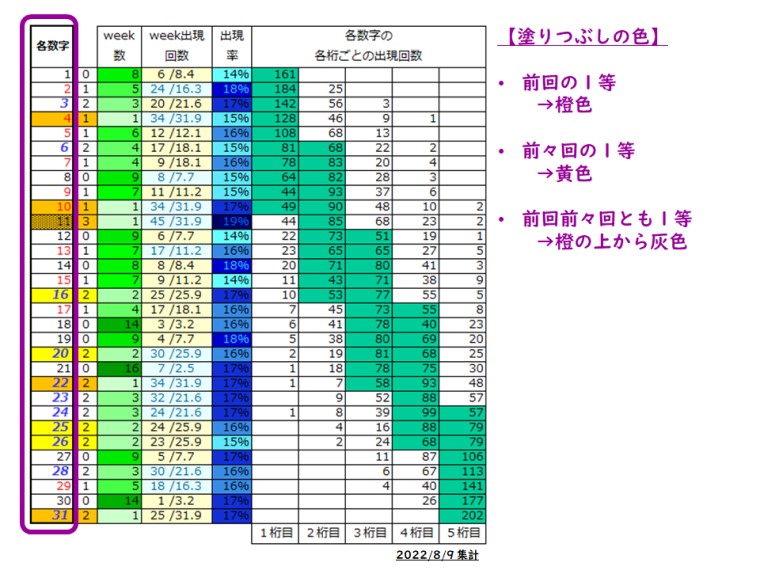
予想をする回(次回)にとって直近2回前の数字を吟味する作業となる。
下の【事例表】でいえば、「前回の1等」が ④ ⑩ ㉒ ㉛ となり、「前々回の1等」が ⑯ ⑳ ㉕ ㉖ となる。ただし、⑪は「前回・前々回とも1等」へ分類する。「前回の1等」と「前々回の1等」はよく出現するので重要なファクターだ。
| 回別 | 1桁目 | 2桁目 | 3桁目 | 4桁目 | 5桁目 |
|---|---|---|---|---|---|
| 前々回 | ⑪ | ⑯ | ⑳ | ㉕ | ㉖ |
| 前回 | ④ | ⑩ | ⑪ | ㉒ | ㉛ |
| 次回 | - | - | - | - | - |
※より実践的な事例はコチラ→「直近50回の発生データ」
「直近2回での出現」とは、上記ファクターの組み合わせでパターンを設定し、予想へ利用する考え方。以下の6パターンだ。
ただし、〖W2作戦〗にチャレンジ中
2024年8月から〖W2作戦〗にチャレンジしている。上記の色のパターンを活用した、排他的で確率的に割り切った作戦だ。購入口数も今では「30口/週」になった。結構リスクがあるので少々心配している。もしこの作戦で当選を果たせたら、このページを大幅修正しようと思う。
2) 直近7回での出現特性
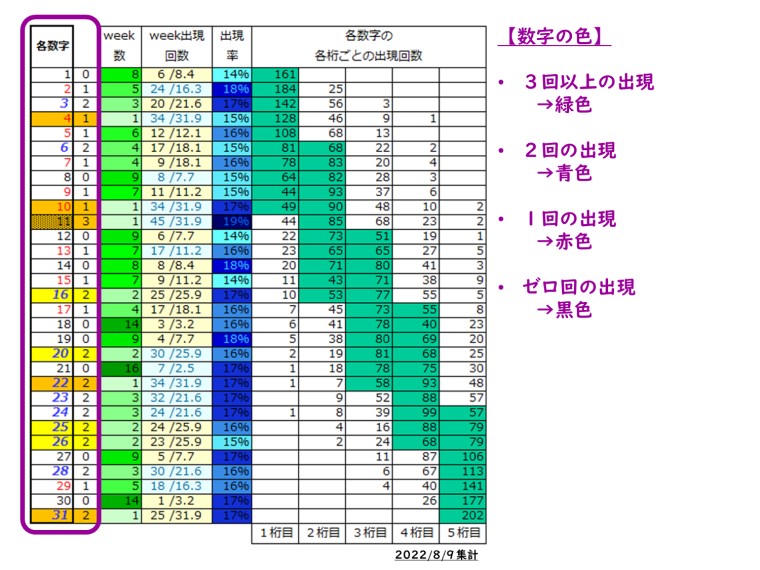
①から㉛の数字それぞれで「直近7回以内に何回発生しているか」を観察している。3回以下を細かく分けてあり、予想フォーマットの中では以下の名前をつけて分類した。
当せんNoは、必ずこれら4種類の数字で構成されるので、4種類がどう配置されるかを予想するのだ。
| 回別 | 1桁目 | 2桁目 | 3桁目 | 4桁目 | 5桁目 |
|---|---|---|---|---|---|
| ・ | ④ | ⑩ | ⑨ | ⑳ | ㉘ |
| ・ | ③ | ⑦ | ⑨ | ⑭ | ⑮ |
| ・ | ⑤ | ⑫ | ⑲ | ⑳ | ㉗ |
| 7回前 | ① | ⑭ | ⑯ | ⑰ | ㉒ |
| 6回前 | ⑨ | ⑬ | ⑮ | ⑱ | ㉘ |
| 5回前 | ③ | ⑤ | ⑪ | ⑳ | ㉓ |
| 4回前 | ⑯ | ㉕ | ㉖ | ㉙ | ㉛ |
| 3回前 | ⑥(0) | ⑦(1) | ⑯(2) | ⑰(1) | ㉒(1) |
| 前々回 | ③(2) | ⑳(2) | ㉓(1) | ㉔(0) | ㉘(1) |
| 前回(事例) | ⑪(1) | ⑯(3) | ⑳(3) | ㉕(1) | ㉖(1) |
| 今回(事例) | ④(0) | ⑩(0) | ⑪(2) | ㉒(2) | ㉛(1) |
3)「桁」ごとに見出す安定性
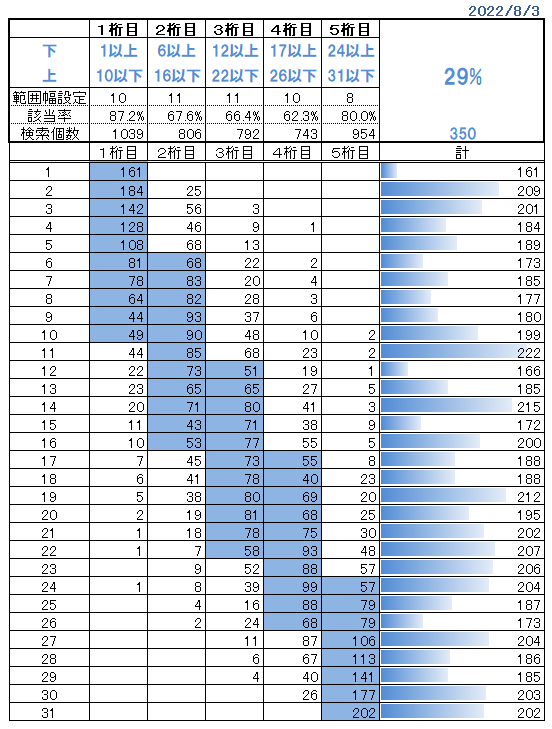
五つの当選数字は「小さい順に並べ替えられている」ので、各「桁」ごとにクセや特性が出てくる。これまでのデータから、そのクセや特性を読み取って決めた条件が上の表にある「上限」と「下限」だ。
この上下限設定を使ってパターン分けし、予想に利用する。
- 外れる桁がある回を 「相応なパターン」 と分類し、
- 外れる桁が無い回を 「片寄ったパターン」 と分類する。
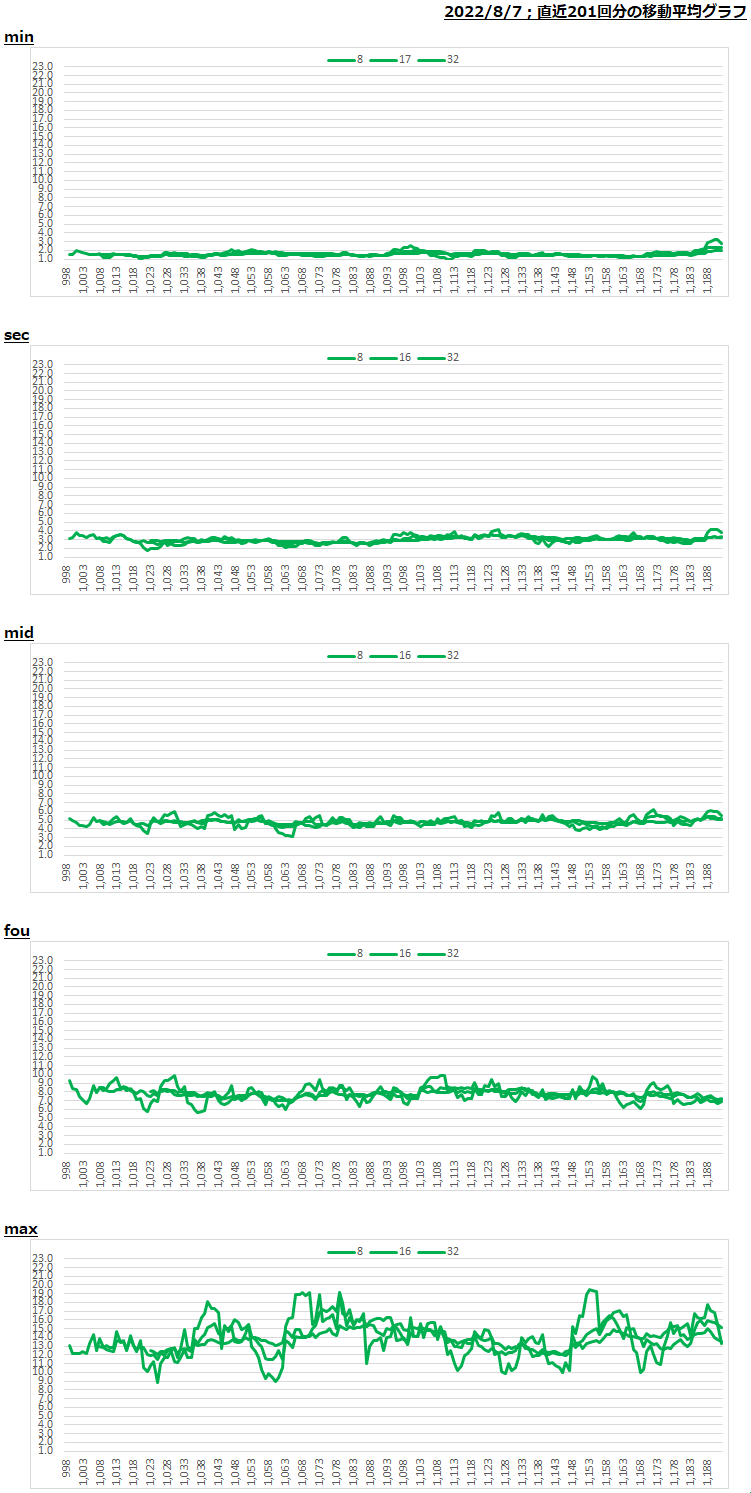
条件は たまに見直ししてて、上表は 2022年8月3日時点での上下限だ。別途「直近201回分の移動平均グラフ」も参考にして設定してある。この五つの上下限を全て満たす可能性は当時で 約29%であった。下のデータ表、
| 1桁目 | 2桁目 | 3桁目 | 4桁目 | 5桁目 | |
|---|---|---|---|---|---|
| 上限 | ①以上 | ⑥以上 | ⑫以上 | ⑰以上 | ㉔以上 |
| 下限 | ⑩以下 | ⑯以下 | ㉒以下 | ㉖以下 | ㉛以下 |
| 相応のパターン | ⑩(〇) | ⑮(〇) | ⑯(〇) | ㉖(〇) | ㉙(〇) |
| 片寄ったパターン | ②(〇) | ⑨(〇) | ⑬(〇) | ⑯(×) | ㉒(×) |
| 相応のパターン | ⑦(〇) | ⑩(〇) | ⑳(〇) | ㉒(〇) | ㉘(〇) |
| 片寄ったパターン | ③(〇) | ⑦(〇) | ⑨(×) | ⑭(×) | ⑮(×) |
4)「week数」から見出す安定性
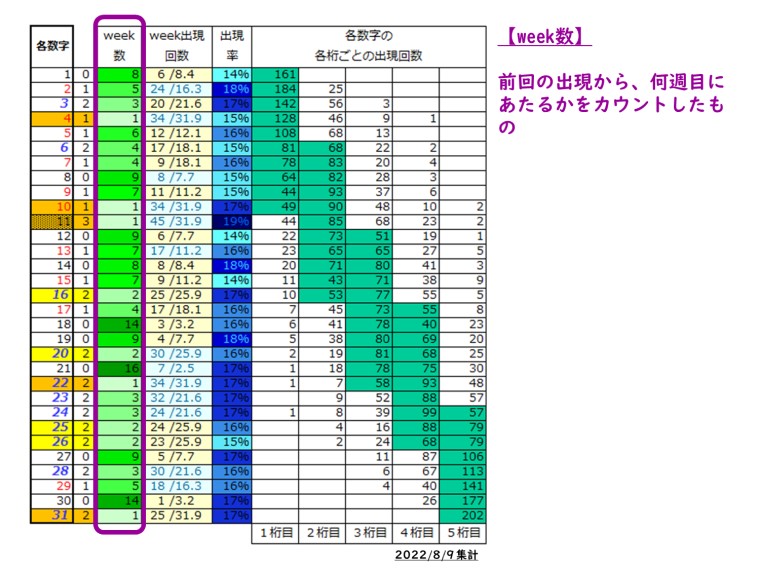
全31数字 それぞれにおいて、前回の出現から何週経過しているかを数えたものが「week数」だ。出現から出現までの回数とも言える。
11回分の抽せんデータを抜き取って事例表にしてみた。数字の隣、カッコ内が(week数)だ。
| 検出 カウント | 1桁目 | 2桁目 | 3桁目 | 4桁目 | 5桁目 |
|---|---|---|---|---|---|
| 事例1 | ④ | ⑩ | ⑨ | ⑳ | ㉘ |
| 事例2 | ③ | ⑦ | ⑨(1) | ⑭ | ⑮ |
| 事例3 | ⑤ | ⑫ | ⑲ | ⑳(2) | ㉗ |
| 事例4 | ① | ⑭(2) | ⑯ | ⑰ | ㉒ |
| 事例5 | ⑨(3) | ⑬ | ⑮(3) | ㉔ | ㉘(4) |
| 事例6 | ③(4) | ⑤(3) | ⑥ | ⑪ | ㉓ |
| 事例7 | ② | ㉕ | ㉖ | ㉙ | ㉛ |
| 事例8 | ⑥(2) | ⑦(6) | ⑯(4) | ⑰(4) | ㉒(4) |
| 事例9 | ③(3) | ⑳(6) | ㉓(3) | ㉔(4) | ㉘(4) |
| 事例10 | ⑪(4) | ⑯(2) | ⑳(1) | ㉕(3) | ㉖(3) |
| 事例11 | ④(10) | ⑩(10) | ⑪(1) | ㉒(3) | ㉛(4) |
ここで算出した「五つのweek数」を小さい順に並べ替えて次の手順に入る。
並べ替えた week数は小さい順に「min → sec → mid → fou → max」と位置づけ、各位置ごとの特性やクセを観察した。そして、安定する「上限」と「下限」を設定したんだ。
| 並べ替え | min | sec | mid | fou | max |
|---|---|---|---|---|---|
| 上限 | 1以上 | 1以上 | 3以上 | 5以上 | 10以上 |
| 下限 | 3以下 | 5以下 | 7以下 | 10以下 | 20以下 |
| 事例9 | 3(〇) | 3(〇) | 4(〇) | 4(×) | 6(×) |
| 事例10 | 1(〇) | 2(〇) | 3(〇) | 3(×) | 4(×) |
| 事例11 | 1(〇) | 3(〇) | 4(〇) | 10(〇) | 10(〇) |
この上下限を外れる桁が「ある回」と「無い回」を分岐点として、「相応なパターン」になるのか、「片寄ったパターン」になるのかを予想する。上の事例表でいうと以下の分類になる。
- 事例11は全ての桁が範囲内=「相応なパターン」
- 事例9と事例10は範囲外あるので=「片寄ったパターン」
上下限は たまに見直ししてて、上表は 2022年8月7日現在で使用中のもの。下図の「分析表」と「移動平均グラフ」で検討したものだ。五つの上下限を全て満たす可能性は約27%である。

5) week出現回数と、その平均との関係
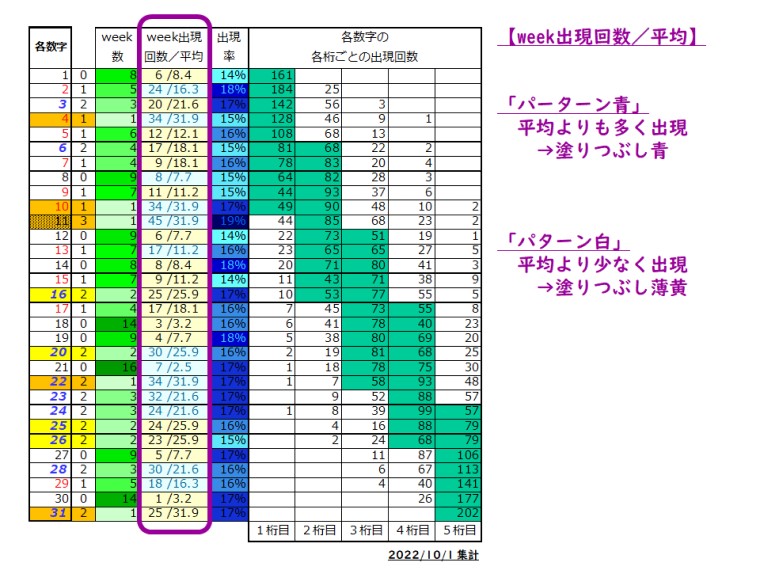
前述した「week数」とは似ているけど違う。week出現回数は、「全31数字それぞれが、各week目ごとに何回出現しているか」をカウントしたデータだ。各week目ごとに全体の平均値も算出してあって、平均値を境にして以下の分類をしている。
- 平均よりも多く出現していたら「パターン青」
- 平均よりも少なく出現していたら「パターン白」
当せんNoは必ずこれら2種類の数字で構成されていて、どのくらい比率で混ざり合うかが予想のいち材料となる。基本的には、「2:3」か「3:2」を狙っていく。この2条件で65%くらいの発生率だからね。予想のときは作業テーブル上で「week出現回数の発生パターン」として管理している。
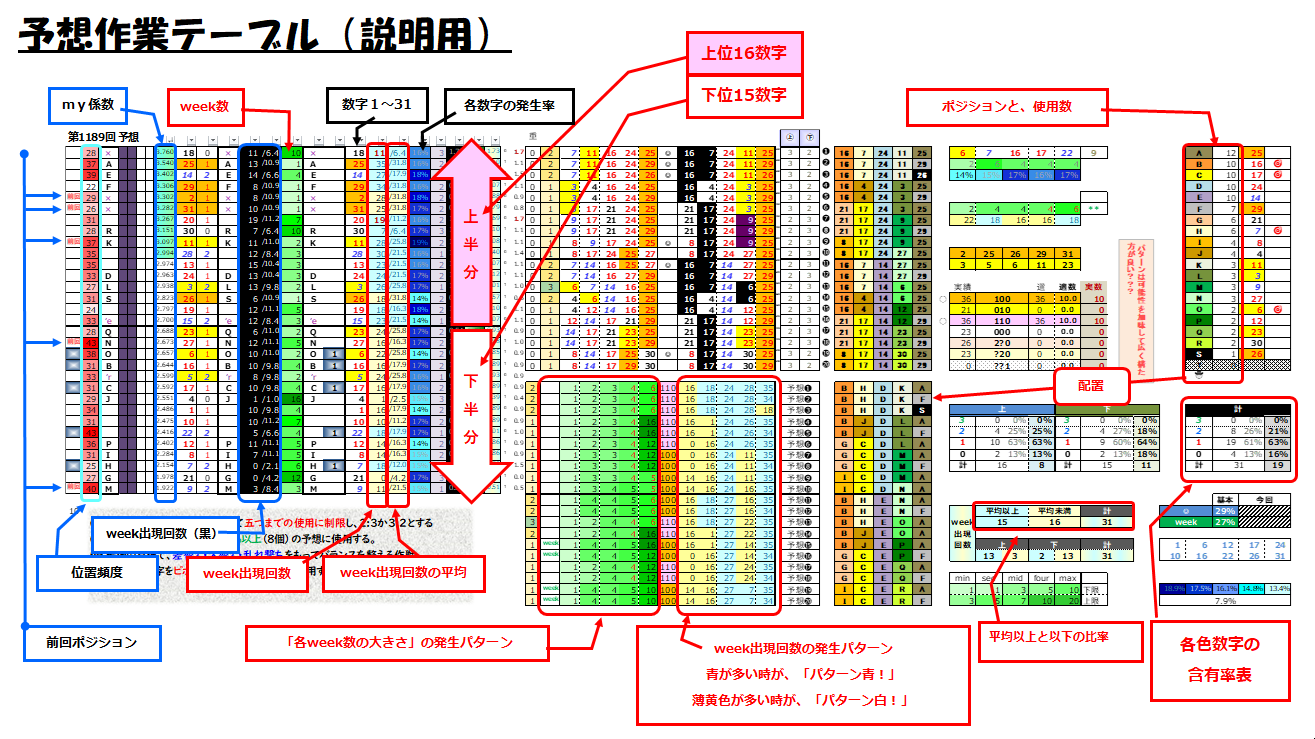
6) 出現率から見出す特徴
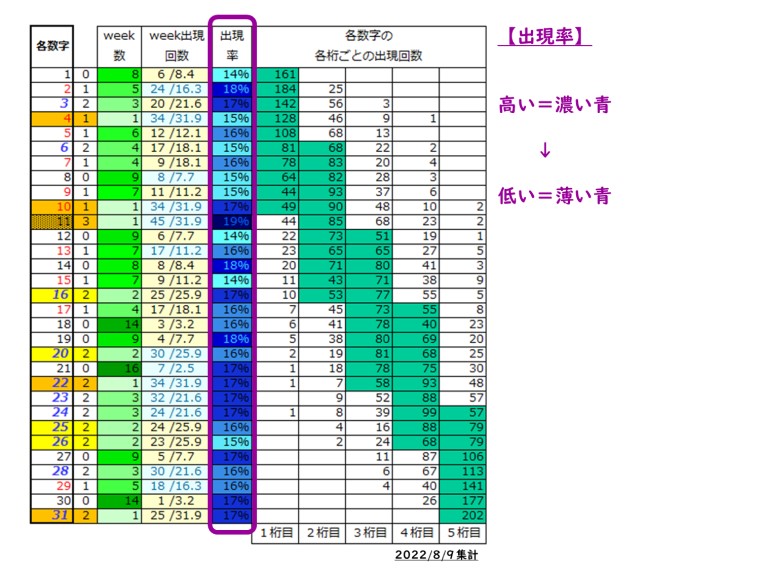
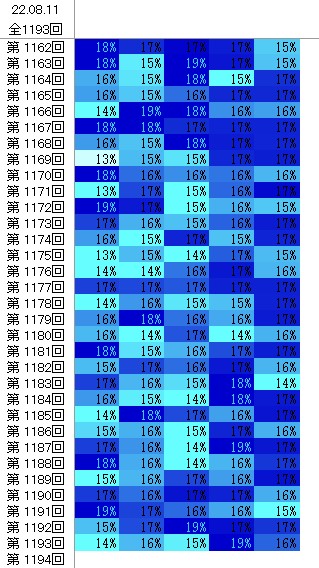
ここでは 全31数字それぞれ(各数字)が持つ「出現率」がどのように並ぶかを予想する。例えば、1193回の抽選で⑤が189回出現していれば、189÷1193で「出現率≒16%」だ。
これまでの当せんNoの出現率の分布実績は全て記録してある。この実績を参考にして、予想する数字は「ありがちな並び」になるように配慮する。下の図は、これまでの出現率分布を抜粋したものだ。
階級は、12%、13%、14%、15%、16、17%、18%、19%の八つにした。図からも解るように、案外、毎回「バランスよく並びがち」だ。
主軸を固める(手順②)
①で決めたコンセプト通りの予想にするために、守らねばならないルールが発生する。この時、優先して先に固める(決める)条件を「主軸」と呼んでいる。
「主軸」として真っ先に決める項目は、上記に記した「コンセプト1 によるパターン選定」だ。以下の六つから、採用するパターンを選ぶ。
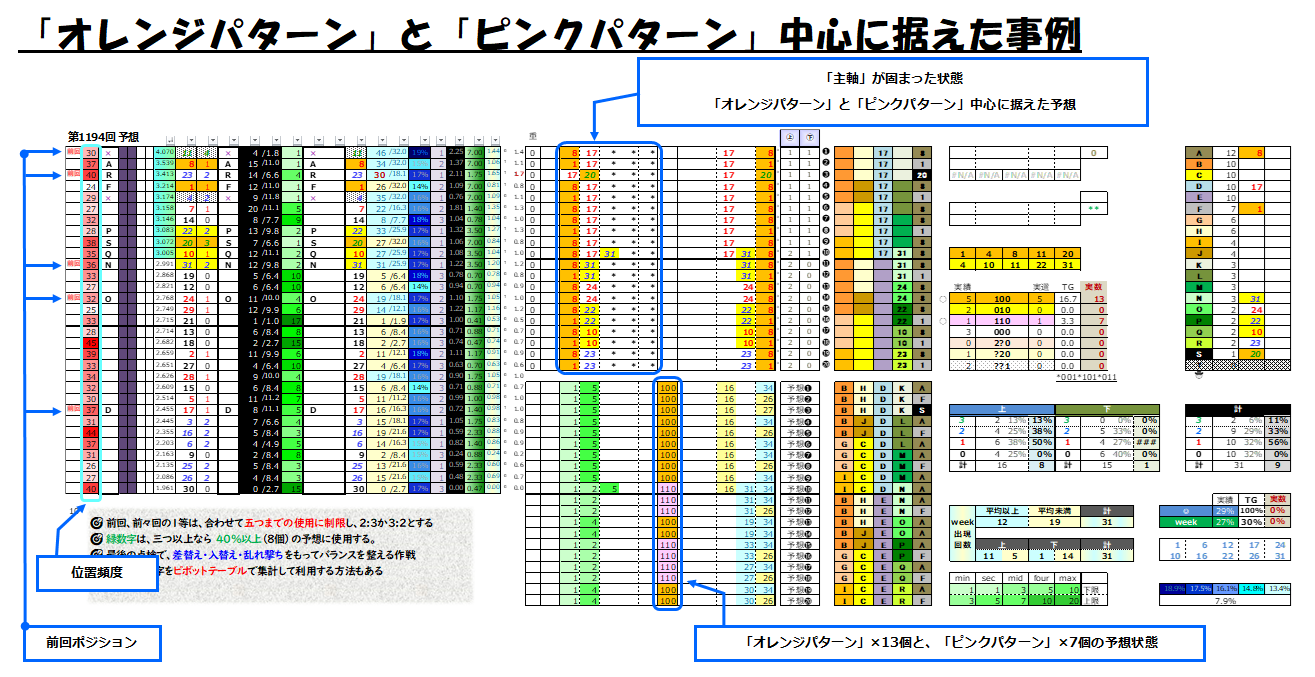
前回の当せんパターンからデータ分析して実績あるものを選ぶ訳だが、この中でも「オレンジパターン」と「ピンクパターン」中心に据えた予想を基本としている。ホントは「前回の1等」だけに絞りたいのだが、「前々回の1等」も結構よく出るから絞りすぎも良くないと考えている。下の図が、「主軸」を固め終えた状態だ。
ただし、〖W2作戦〗にチャレンジ中
2024年8月から〖W2作戦〗にチャレンジしている。購入口数も今では「30口/週」に増加した。新しい項目「前回のポジション」なんかも活用しているが、試験登用中の内容だから ここでの説明は割愛した。もしこの作戦で当選を果たせたら、このページを大幅修正しようと思う。
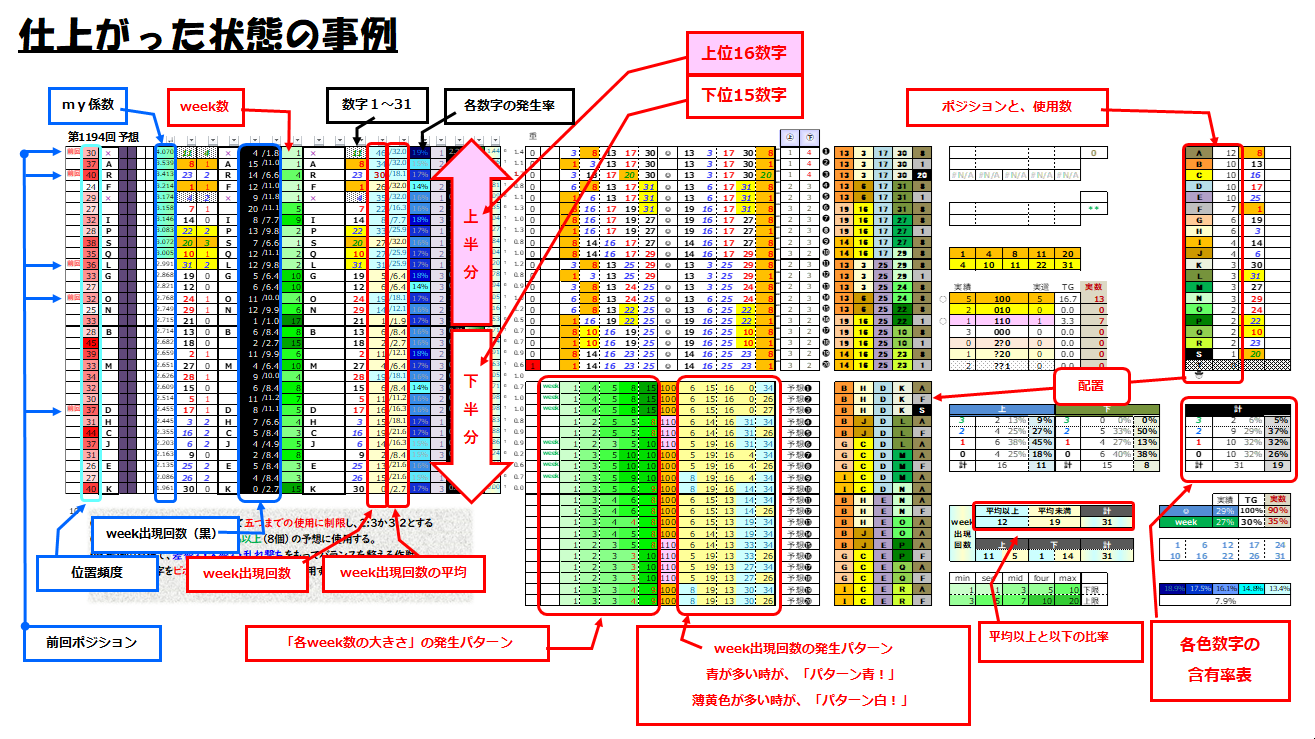
仕上げ(手順③)
①で決めた「コンセプト2~6」の通りになるように、且つ②で固めた「主軸」が崩れないように数字を選んで、そして並べていく。この時「コンセプト2~6」の全ての条件を満たすように予想を仕上げるのは結構大変。現実的にはこの段階で「主軸」を修正せざるを得なくなるケースも多い。下の図が、20個の予想すべてが仕上がった状態だ。
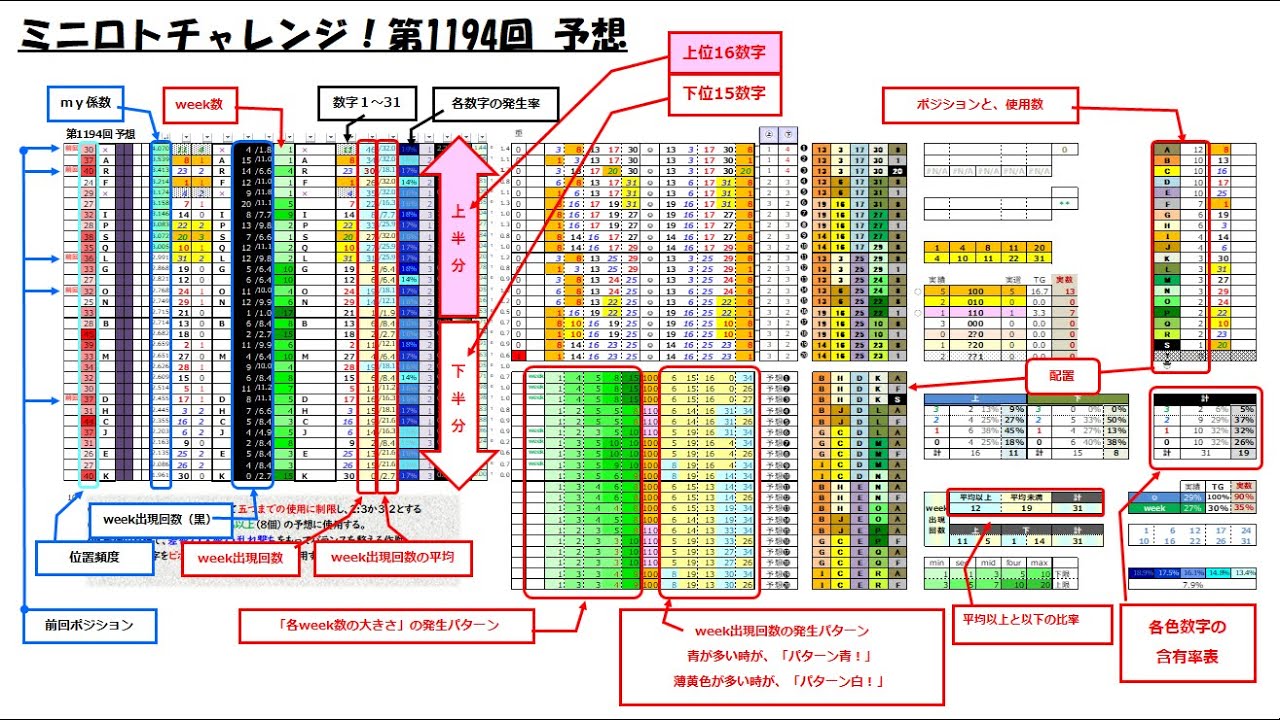
手順動画(YouTube)
下の動画は、第1194回の事例。標準書通りに予想を勧めた事例だ。
予想完了(手順④)
しばらく眺めて、ミスや忘れ物が無いか点検をする。めったにないが、ここで何か気に入らなくて修正する事もある。例えば下図。「予想⓴」は過去(1999年、第18回)に当選した実績を持つNoである。これが気に入らない場合は、数字を入れ替えるか、並べ替えるかして解消する。マトリックス方式なので、他の19個の予想にも影響を与えてしまうのを嫌う場合はそのまま行っちゃうこともある。
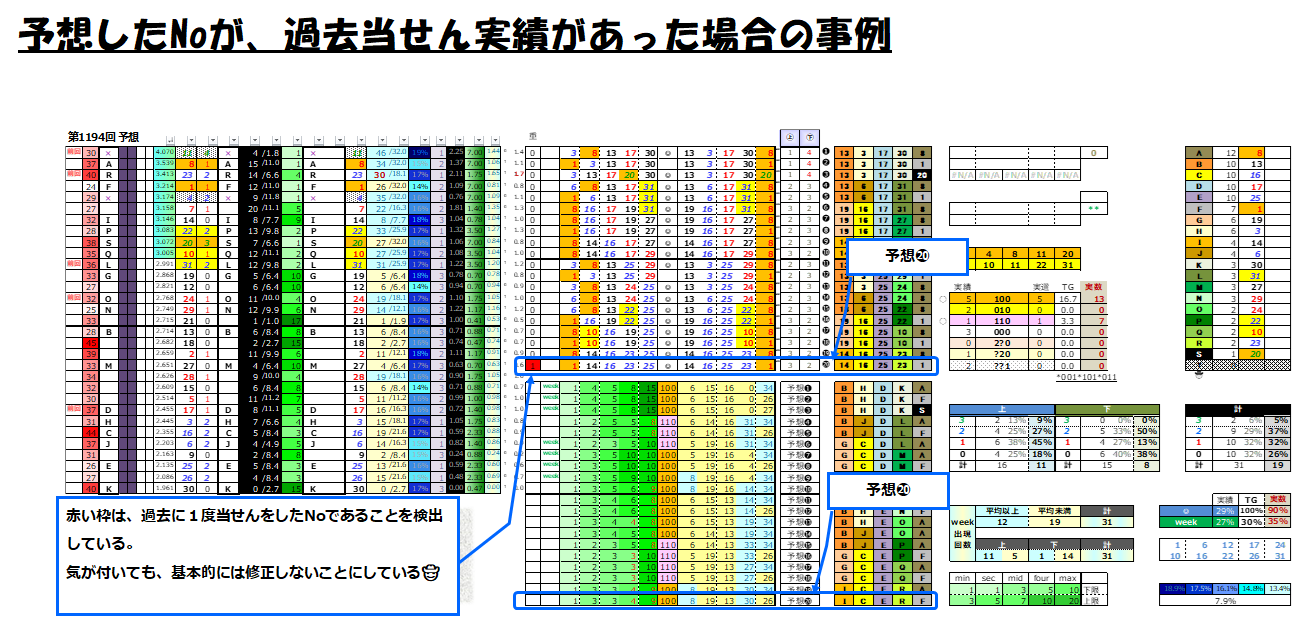
予想結果について
結果は、予想からの流れが見れる記事にして毎週記録している。今は「当たりっぷり」のタグ内に記事は無いが、いずれブチ込んでやる。
まとめ
まずは1度ミニロトを当て、「ロト6」や「ロト7」にも挑戦したいと考えている。まずはミニロトの初当たり🎯を実現せねばならない。
「ロト6進出の準備!」の、そのまた準備として「ミニロトの予想手順」をここに整理した。進出の際にはきっと大いに役に立つだろう。しかし やはりここに集約するが、まずはミニロト1等当選を果たさねば何も始まらない。

※
このブログには、特有の単語や言葉づかいがあります。
それぞれ 用語説明ページ⮭ へリンクさせ、説明をしています。
※注;予想サイトではありません
このブログは、私個人の方法論とトライ&エラー記録を公開し、くじ当せんの困難さを表現するものです。
他者へ「攻略方法」などを促しているものではありません。
「当選確率のアップ」などは致しておりませんのでご注意ください。
