思い立って『統計学』を勉強することにした。
動機は不純で、少しでも「ミニロト予想」に役立てばとの想いから。でも知っていれば絶対に仕事なんかにも役立つだろうし、やって損するものでもない。そう考えると思い切って行動できた。
まずは、統計検定【4級】に合格することを目標にする。このページはノート替わりの「勉強ページ」だ。日本統計学会の公式認定問題集(参考書)を使って勉強した要点を整理していく。
勉強方法の検討
勉強方法の選択肢として、探し当てた勉強方法はこの四つ。
- 新出題範囲対応 例題集(ネット上)
- 過去問題(ネット上)
- 日本統計学会認定の標準テキスト
- 日本統計学会認定の公式問題集
この内の③と④で勉強することにした。「公式問題集を、標準テキストで調べながら解く」 まずは、これをやってみる。もちろん買った。時間をかけるからにはきちんと勉強したい。
教科書と問題集
③日本統計学会認定の標準テキスト

④日本統計学会認定の公式問題集

なるほど統計学園
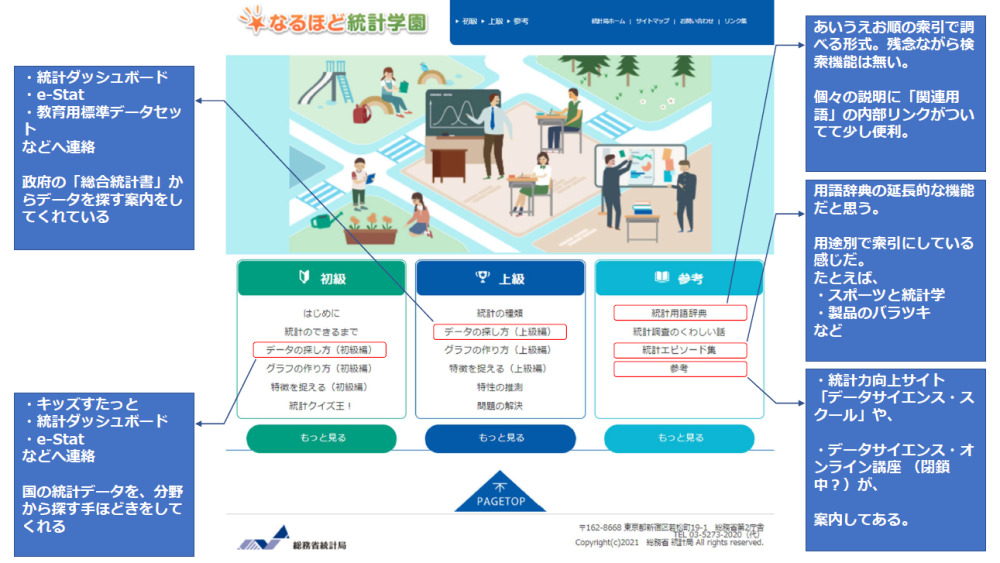
上記で買った教科書「データの活用」で紹介してあったサイト「なるほど統計学園」。総務省が子供向けに開設したようだが、こんなの子供が読むとは思えんな。
初級と言っても、語り口がやさしいだけで結構むずかしいことが書いてある。むしろ、おじさんくらいの方が ちょうど良いのではなかろうか。
たとえば、統計検定の勉強過程で 困ったり、疑問なんかが出てきたとする。このサイトの中を探して解決できるようになったら、もうずいぶん知識がついている段階だろう。このサイトを使いこなせるようになる過程で、かなり統計の理解レベルが上昇すると思う。ただし、サイト内検索機能がないのが大変残念だ。
勉強ノート
当ページを4級受験のノート替わり使う。各年ごとに、調べなきゃわからなかったことや、勉強しなきゃ知れなかったことを書き留めていく。
用語
覚えておきたい単語。忘れないようにここへ書き記しておくべし。
PPDAC
有名なのは「PDCA」で 生産的活動のための正しい行動パターンを説明したもの。Plan→Do→Check→Actionの頭文字だ。
「PPDAC」は 問題を解決に導くための行動パターンを説明したものと考えよう。常に意識して行動出来れば、失敗も減るだろう。「なるほど統計学園」にわかりやすい説明があった。→コチラ
- Problem
問題を明確化して、仮説を立てる - Plan
不足している知識を取得し、データの具体的な収集方法を計画する - Data
データを収集し、表を作成するなどして、整備する - Analysis
グラフを作成し、状況を見えるようにして、問題を分析する - Conclusion
分析した結果を解釈し、仮説の評価を行い、新たなアイデアなども含め、レポートに整理する
確率の記号「P」
計算式なんかで、確率は「P」で表される。「probability」の頭文字なんだって。覚えておきたい。
統計分析の分類
●記述統計
手元にあるデータの持つ情報を明らかにするための分析。
●推測統計
手元にあるデータは全体の一部と考え、一部のデータから手元にない全体を推測する分析。抜き取り検査的な。
データの種類
| 性質 | 事例 | |
|---|---|---|
| 質的データ | 分類や種類 | 国籍、血液型、科目、趣味、学年、生まれ月など ※ 見た目が数字の項目に注意! (和や平均に意味をなさないものは質的データ) |
| 量的データ | 数量 | 身長、体重、気温、本数、点数など ※ 量的データをさらに分類 ・連続データ →身長、体重、時間、気温など ・離散データ →サイコロやトランプの数字、人数、個数、 試験の点数、そしてミニロトの出目など |
代表値
集団の中心的傾向を示す値を「代表値」といい、主に平均値、中央値、最頻値などを差す。
参考になった記事
- 解りやすかった記事→量的データと質的データの違い
- おもしろかった記事→データを読む力を高める
同様に確からしい
直訳すると「同じように起こる可能性がある」という意味と解釈する。サイコロ=確率1/6を使った問題で出てくる可能性が高い。「確率通りの動きをするサイコロだよ」とか、「出る数字に偏るような不良品ではないよ」などと言いたいときに使われる表現。
移動平均
たとえば、EXCELでいう下図。ミニロト予想の実戦でも運用しながら研究中だ。→実戦使用の事例はコチラ
※ 最新~ n=5レンジ
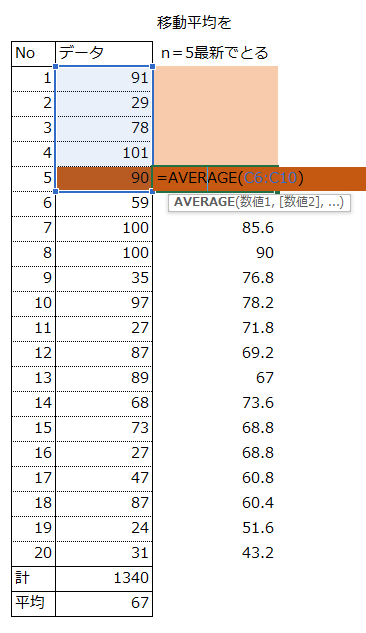
※ ~中央~ n=5レンジ

標準偏差
標準偏差とは、(測定値と平均値との差)² を合計して、データ(測定値)の個数で割り、その平方根をとった値。
ベル型の特徴を持つ正規分布ならば、
「平均値ー標準偏差」と「平均値+標準偏差」の区間に全体の68%の値が含まれることになる。
(日本統計学会認定の標準テキスト「データの活用」P67より)
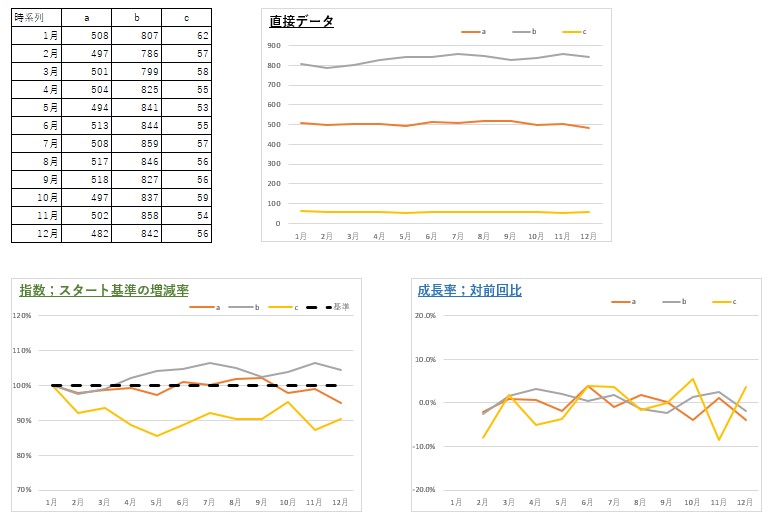
指数と成長率
時系列データにおける用語。
●指数とは
自分で選んだ任意のポイントを基準に決めて、他のポイントを相対値で表現したもの。ある一点からの「増減率」だ。倍率的なこと。基準点を「100」に置き換えて、他点を百分率で表すことが多い。
●成長率とは
上記の任意のポイントを「ひとつ前のデータ」に限定された「増減率」の形。たとえば、対前年比などがよく目にする事例。
度数分布
「中央値」
データの max値 と min値 の中央値だと思ったら違った。頻度総数(データの大きさ)の「真ん中位」が含まれる階級の事だった。
下表➊で例えれば、データの大きさが 20(偶数)なら、10位と11位が含まれる階級そのものを指す。25.5が正解となる問題もある。
| データ (範囲) | 頻度 | 中央値 |
|---|---|---|
| 5~10mm | 0 | |
| 10~15mm | 1 | |
| 15~20mm | 2 | |
| 20~25mm | 8 | 👈10位を含む |
| 25~30mm | 6 | 👈11位を含む |
| 30~35mm | 3 | |
| 35~40mm | 0 | |
| 40~45mm | 0 | |
| 計 | 20 | 👈データの大きさ |
下表➋例えれば、データの大きさが 31(奇数)なら 16位だ。総数が偶数と奇数で変わる事に注意。
| データ (項目) | 頻度 | 中央値 |
|---|---|---|
| タイプA | 1 | |
| タイプB | 4 | |
| タイプC | 10 | |
| タイプD | 2 | 👈16位を含む |
| タイプE | 1 | |
| タイプF | 4 | |
| タイプG | 7 | |
| タイプH | 2 | |
| 計 | 31 | 👈データの大きさ |
「このデータの中心は?」と問われたときは「中央値」と回答するのが良い。特に左右均等でない歪んだ分布では、平均値ではなく中央値が有効である。
(日本統計学会認定の標準テキスト「データの活用」P213より)
「階級値」
問題の文中に「階級値」とでてきたら、「階級の下限と上限の真ん中の値」のことを指す。上の表➊で考えると、下表❸となる。
| データ (範囲) | 階級値 |
|---|---|
| 5~10mm | 7.5 |
| 10~15mm | 12.5 |
| 15~20mm | 17.5 |
| 20~25mm | 22.5 |
| 25~30mm | 27.5 |
| 30~35mm | 32.5 |
| 35~40mm | 37.5 |
| 40~45mm | 42.5 |
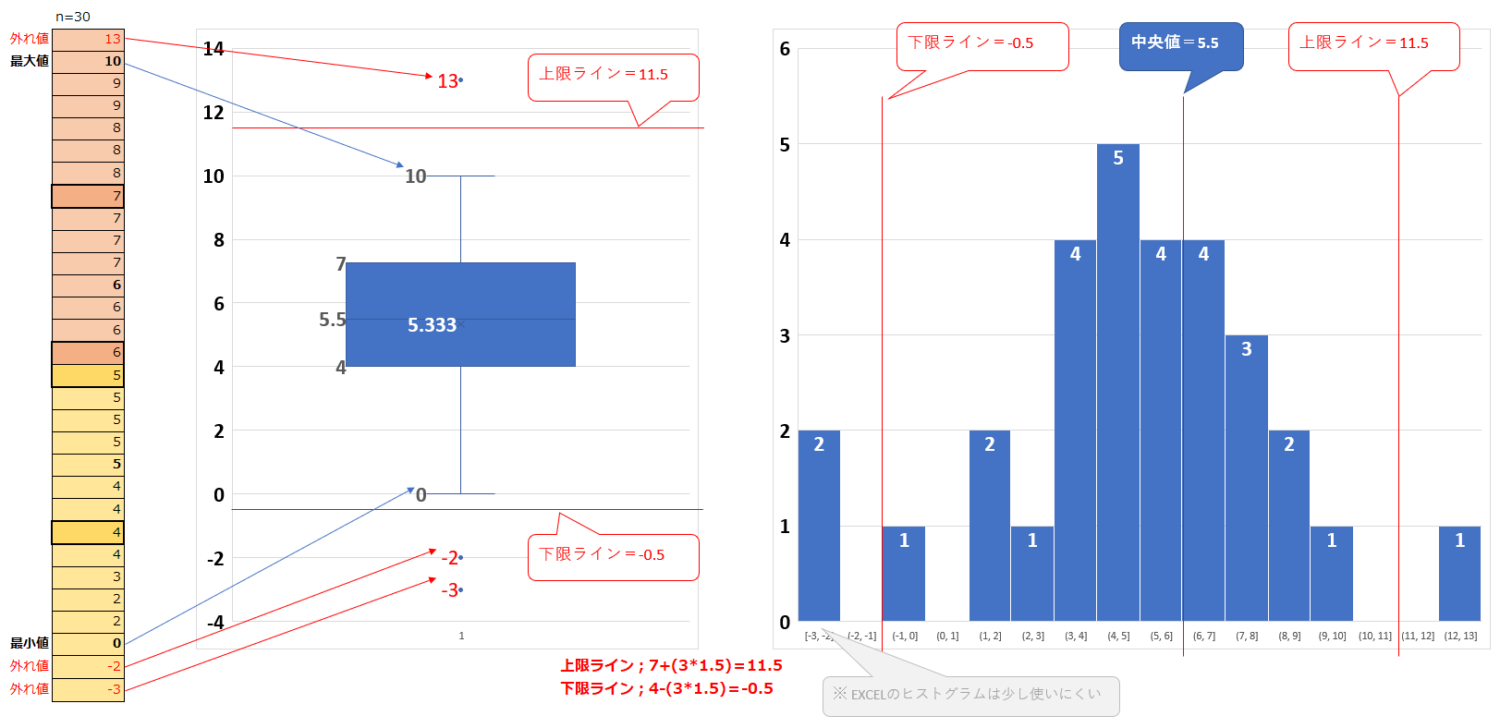
「範囲」と「外れ値」
度数分布表は奥が深い。簡単そうで案外ややこしかった。度数分布における「最大値」と「最小値」、そして「外れ値」。何度も間違えた。なんなら今でも間違えてしまう。
ここに復習をしておこう。もう間違わないように。
●「四分位範囲」と「範囲」
(四分位範囲)=(第三四分位数)ー(第一四分位数)
(範囲)=(最大値)ー(最小値) ※ 外れ値を除く
※この資料がわかりやすかった!→統計WEB
●「最大値」「最小値」「外れ値」
今回、実感的に感じ取り、とても参考になったのは「外れ値」だ。実務でデータを扱っているが、この「外れ値計算」の存在を知らなかったので 直感的に察知して惑わされないように頑張ってた。
四分位範囲の「1.5倍」を各四分位数へ足したラインを上下限とすればいいのか。よく解ってなくて間違えたのは、「最大値」と「最小値」。ポイントは以下だった。
- 最大値は?の問題に、間違って「上限ライン」の計算値をそのまま回答して間違った。正解は、「上限ライン」の内側にある「数値」なのだ。
- 最小値は?の問題に、間違って「下限ライン」の計算値をそのまま回答して間違った。正解は、「下限ライン」の内側にある「数値」なのだ。
ポイントを自分でグラフ化。共通の n=30データで「箱ひげ図」と「ヒストグラム」を書いて視覚的な理解を試みた。この図表は「手計算」で出した値に近づけてあるが、EXCELは手計算と違ってくるので要注意だ。詳しくは、後の項目「箱ひげ図」で考察する。
「平均値」と「外れ値」
「平均値の算出時に外れ値は除くのか」で、少々迷った。
いろいろと調べた結果、大切なのは『なぜ外れたのか』のようだ。真の実力を診断する際は、故障や不具合の時に取れたデータは当然外すべきでしょう。でも、状況把握が目的ならトラブル込みで考えねばならない時もある。答えは、「場合による」なんでしょう。
- 統計検定4級の公式問題集では「外れ値も平均算出に入れる」としてある。公式の設問なんかで迷ったときは入れた方が良さそうだ。(P265;2019年11月-問9の解説より)
- 外れ値が存在する場合の「分析方法」としては、『外れ値を除いた分析』と『外れ値を含んだ分析』と、両方の結果を出すのが良いとあった。
(日本統計学会認定の標準テキスト「データの活用」P213より)
※この資料がわかりやすかった!→統計学が わかった!「外れ値の対策」
分布の特徴 「歪む」と「裾を引く」
分布と特徴を表現する言葉として、「歪む」と「裾を引く」というものが幾度となくでてきた。
たとえば下図のように、左右対称のきれいな正規分布が広がることを言う。図は右に広がっているから、「右に歪む」または「右に裾を引く」と言う。この二つの表現は全く同じことを差していると理解した。
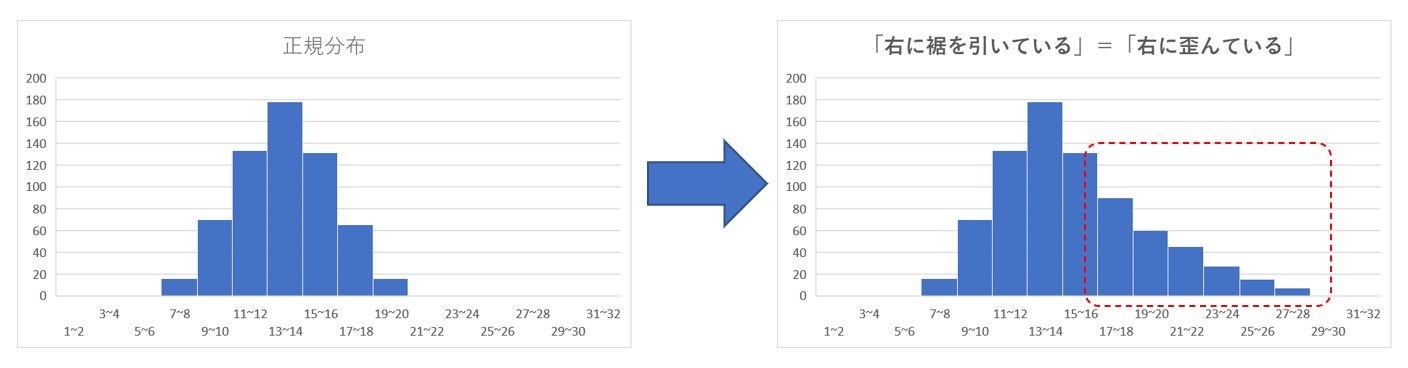
日本統計学会認定の標準テキスト「データの活用」P124~125より
これは使える!箱ひげ図
全然知らなかった。筆者がこどものころの授業では教えられていないと思う。けれど、これはかなり使えそうだ。box plotとも呼ばれる。
【知らなかったので調べた】
すごく解りやすい動画を見つけたのでストック。
【解らなかったので書いてみた】
第一四分位と、第三四分位を EXCELで 算出すると混乱した。手計算した値と どうしても合わなかったので。更に とんでもない事に XCEL同士でも 誤差が出る。「箱ひげ図」と「QUARTILE.INC関数」でも、四分位数に 誤差 が出たケースもあった。
いろいろ調べた結果、「箱ひげ図考案者Tukeyオリジナル」と「QUARTILE.INC関数」で定義に若干のズレがあると理解した。使うシチュエーションは 結局EXCELなので、状況だけは把握しておかねばなるまい。自分でも書いてみる。
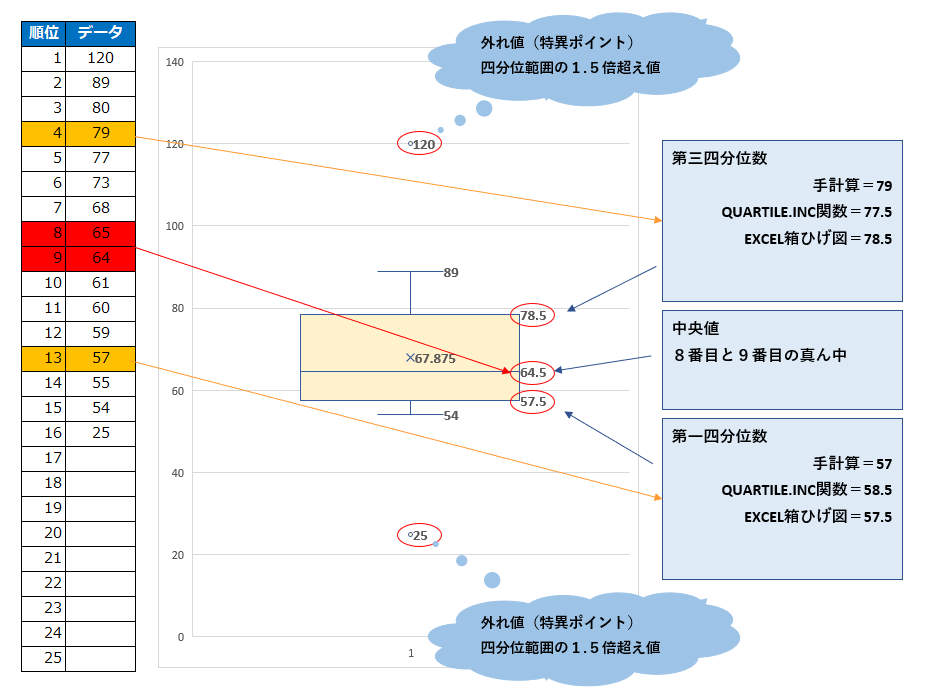
- この資料がわかりやすかった→教師のEXCEL口座
- この資料がわかりやすかった→四分位数の違いについて
【自分のデータでも試してみた】
ミニロト=1,163回分の EXCELデータで作ってみた。
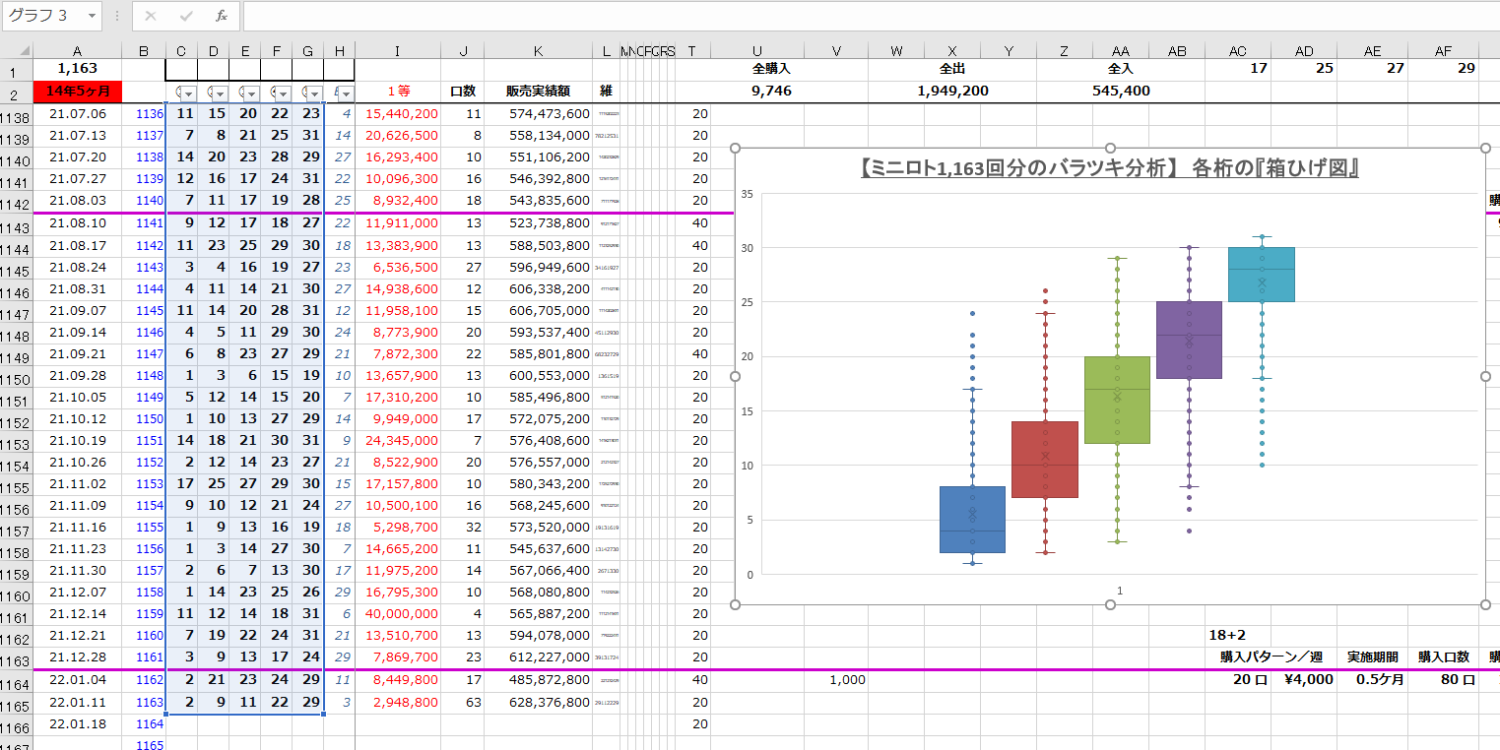
幹葉図(みきはず)
恥ずかしながら、幹葉図なんて知らなかった。数字を分解して、末尾だけを度数分布に並べていく手法。知ってたら便利そう。仕事でも使えそうかというと部署によるか。
| 1の位まで | 小数第1位 | 度数 |
|---|---|---|
| 0 | 168 | 3 |
| 1 | 0 | 1 |
| 2 | 0 | |
| 3 | 89 | 2 |
| 4 | 0 | |
| 5 | 0 | |
| 6 | 2 | 1 |
| 7 | 96 | 2 |
| 8 | 0 | |
| 9 | 357 | 3 |
| 10 | 72111 | 5 |
| 11 | 4 | 1 |
| データの | 大きさ | 18 |
データ
0.1
0.6
0.8
1.0
3.8
3.9
6.2
7.9
7.6
9.3
9.5
9.7
10.7
10.2
10.1
10.1
10.1
11.4
クロス集計表
複数の項目を組み合わせて度数を集計した表。いちばん使う形だろうな。って言うか、これしか使わん。大抵はコレでこと済んでしまう。散々使ってきてたのに名前は知らなかった。
コレなんかそうでしょ👇このブログ内でもいっぱい使ってる(笑)
国勢調査
こんな問題出る?!テキストにも載ってない!!検定すべき内容なのか?不思議。
- 調査対象は、同居している家族単位である。生活費を仕送りしていたとしても、別居していれば別世帯としてカウントされる。
- 常住していれば、外国人も調査対象である。該当住居に3カ月以上住んでいるか、または住む事になっているかが条件である。
- 2015年(平成27年)から、オンライン調査も行っている。
- 調査は5年に一度、西暦で5の倍数年に実施される。末尾=0の年は「大規模調査」、末尾=「簡易調査」となっている。初回は1920年(大正9年)に行われた。
- 調査の目的は、国内の人および世帯の実態を把握し、各種行政施策その他の基礎資料を得ることである。
ちょっと脱線!
独学なのでのんびりやる。何か気になったらどんどん脱線しよう。
ミニロト確率の分母
筆者の昔のミニロト予想は、全31数字の中から、20個を選び、20口の組み合わせを作っていた。
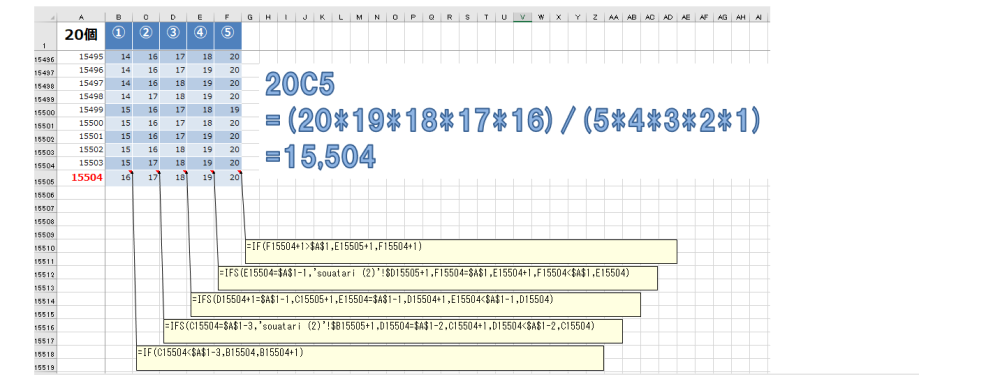
五つの数字がこの中に含まれた場合、どのくらいの当選確率だったのかを計算した。20個の数字すべての組み合わせは何種類あるのかが分母だ。調べると、20個の中から5個取り出し且つ「並べる順序は考慮しない」ので「20C5」となり、15,504種類の組み合わせが正解。簡単に計算できるらしい。
こういうのを、ササっと軽やかにできるようになるため統計の勉強を始めたのだが今はまだできない。後学のため、手計算で全種を並べて『15,504種類』あるか数えてみるとピッタリ合った。手計算と言っても、EXCELの関数を使って下にズルズルっとコピーしたらすぐできる。
●5/20個数字の分母=15,504種類
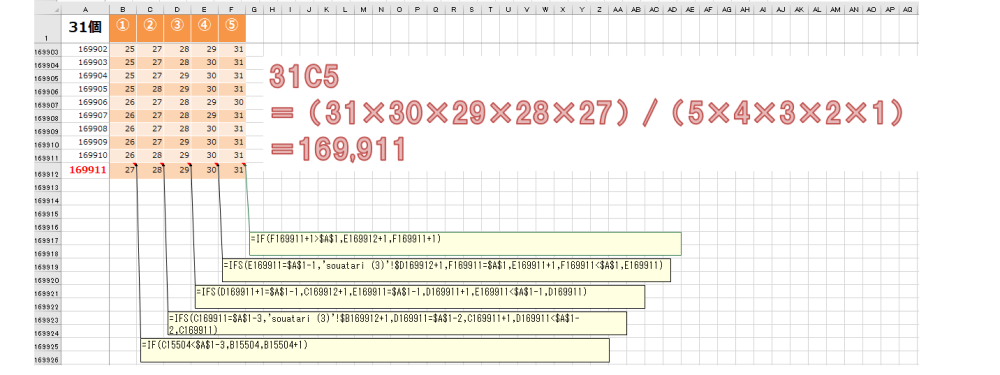
ちなみに、せっかく苦労してEXCEL関数を作ったのでミニロトそのものの数も数えてみた。公式でも言っているミニロトの確率は、「1/169,911」、ぴったり合った!
10年くらい前にもやったことあるけど、あの時はホントに手で並べたのでムチャクチャ時間がかかったのを覚えている。今回はEXCELテクニックも向上してるのですぐ出来た。
●5/全31数字の分母=169,911種類
安心!カンタン?受験の手順
ネットで調べた限りではかなり受験しやすそうで安心だ。
場所や日時は、まず最寄りの会場を自分で選び、選んだ会場で受験日を選べるようだ。(CBT方式試験)いくつか見てみたら、関東から南の地域では だいたい20日/月くらいは試験を受けれる日だった。北日本はあまりやってないみたい。

挑戦は続く!
1度目は不合格
先日、試験を受けて不覚😵にも『不合格』だった。60分で30問、思ってたよりきつかった。三分の二くらいを解いたところで時間切れ。年を取り、処理速度がますます落ちてることをリアルに体感した。頭に無かったけど、よくよく考えると「1問=2分で解かなきゃいけない」んだ。
舐めてました、ごめんなさい。
2度目でなんとか合格!

やっと合格。😅
4級でこんなに苦労するなんて先が思いやられるが、とりあえず良かった良かった。こんな苦労もすべてはミニロトのため。最後に当たればすべてヨシ!
今後は3級にチャレンジ。全体の様子を「統計の勉強をしよう」に記録していきたいが、3級ですでにだいぶん手こずっている。いろいろやりながらだし、何年かかるだろう。

デジタル卒業証明書オープンバッジサービスの開始

2023年12月、一般財団法人統計質保証推進協会が「オープンバッジ」なるものが授与してくれた。
オープンバッジウォレットへ取得した資格のデジタル卒業証明書がたまっていくサービスを開始したそうだ。たかだか4級。しかし、嬉しいものは嬉しい。
