外れモンスター！ shirono-j🤠です。
今週は夢を見たから、いつもと少し違うかも。
誰かとトランプで勝負をしていた。
最後にきわどい選択をして「ハートのＡ」を引いて大勝利。
そんな夢を見て飛び起きた。
「これは何かの予感かもしれない」と燃え上がり、早朝暗いうちからセッセと予想しました。夜にする予定だったのに。（笑）
これで当たったら、ホントびっくりだな！😃
〖購入実績1100〗ミニロト予想
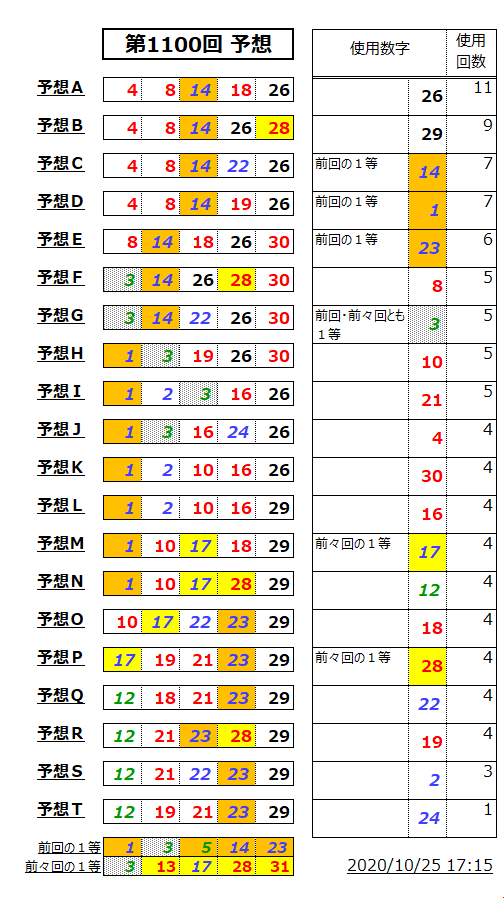
今週はエライ事になったな。
今までずっと避けてきた①②③のそろい踏みがある。
先週の反省で、①の封印は止めるって決めてるしな。
おまけに「ハートのＡ」を引いた夢までみた。仕方ない。
もひとつおまけに、第221回で１度当選している並びも入っちゃったんだよな～。（予想Ｃ）
不思議尽くしの回だな。
これで今回当選してたら、スピリチュアル的なものを信じたくなってくるな～。
心配ないか。むしろ望むところや。
心配なのは⑤が出目ること。
結構迷った末に外したから逃げられるとダメージがでかい。
あとは、
「各week数の大きさ」が相応なパターンで固めたから、逆をつからたら痛いな。
まあ今週も、予想コンセプト変更の初期流動期間。いろいろあるさ！🤠
【実戦結果1100】ミニロト反省
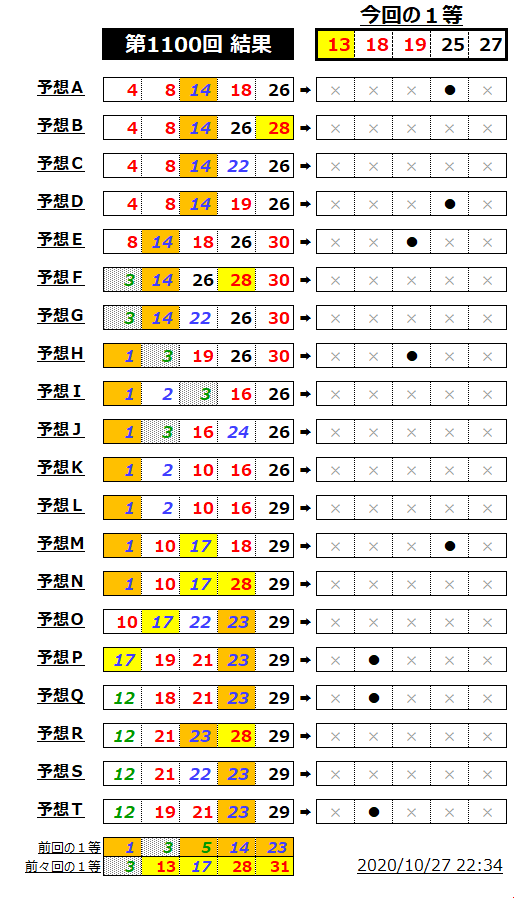
【13年間の成績表】ミニロト実績
ミニロトチャレンジの源泉となるページ。
目標や考え方、ミニロトの概要なんかを整理してあるんだ。
ぜひ、お立ち寄りください🤠（画像をクリック！）
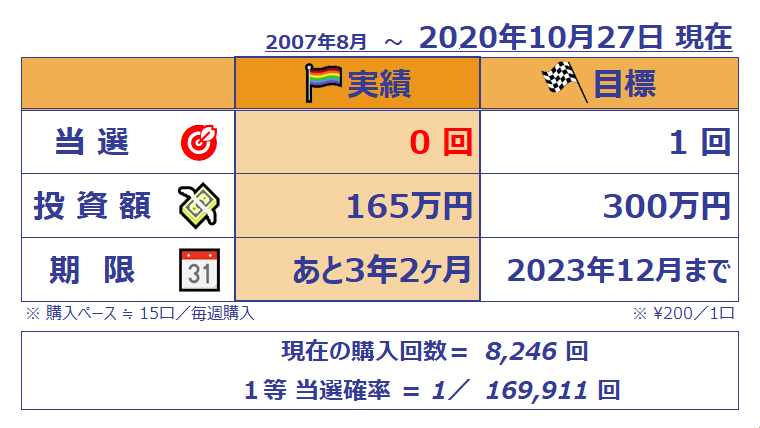
今週のひと言
お金が無くなったら、ミニロトや宝くじもなくなるんだろうね。
意味なくなるもんね。
残念かと言えばそうでもない。ホントにお金も無くなるならね。
お金が無い世の中なんて想像もできないな。どうなるんだろ。
最近は「お金がお金を産む」とか「複利がどうのこうの」とか、わかり難いというか、若いうちから投資しないと大損するぞ！って言われてももう年喰ってるし。
世の中は経済成長する一方で、株価は長期的にみれば絶対に上がるとか、ほんとかよ～って思う。
それは「今」目線の、数百年ていどのデータでしょ。
ホントのところ、どうなんでしょうね。
我迷う。🤠
直近50回の発生データ
直近50回分のデータを羅列。毎週更新していて、「前回の１等」や「前々回の１等」の出現状況を『色』で表現してある。
※
色の意味に興味のある方はコチラ → 直近２回での出現（色のパターン）
統計データ掲示板
ミニロトのために統計の勉強中。少しでも１等当せんへ近づけないか、何とか攻略できないものかと必死にやっている。勉強した中身を利用してデータをグラフ化、最新の状態をここに記録する。愚か者だと人は言うだろうが、勝てば官軍。正義が勝つのではなく、勝った者が正義なのだ。
がんばって最後に勝つ。
度数分布表；全31数字×桁別
全31数字の発生頻度を「桁別」でカウントして整理した集計表。
「計」と「発生率」の列では、以下の書式訳になっている。
- 平均以上値＝ピンク枠で太字
- 最大値＝青枠で太字
- 最小値＝緑枠で細字
- その他＝白枠で細字
出現度数；ヒストグラム
第１回から現在までの「全抽せんデータ」で分析してグラフ化した。出目頻度のヒストグラム（度数分布）を「桁別」で書き出したもの。ピンクの部分が「桁ごと」の度数を表し、グレーの部分は全体を表わす。右側の図は 最近勉強した「箱ひげ図」だ。
気付いたのは以下の2点。
- 桁別なら正規分布に近い
- ５桁目はバラツキが小さい
移動平均と合わせ見ても５桁目はバラツキが小さ目だ。理論的には１桁目と同じはずなんだけどなぁ。よく解らんけどせっかくだから予想へ利用している。
度数分布に関しての私の理解程度はコチラを参照。→ クリック↗
移動平均；折れグラフ
出目頻度の移動平均を「桁別」でグラフ化したもの。過去201回分の移動平均を連続させた 折れ線グラフにしている。以下の３種類を、ひとつのグラフに重ね合わせている感じです。
- 最新～ n=8レンジ（８回移動平均）
- 最新～ n=17レンジ（17回移動平均）
- 最新～ n=32レンジ（32回移動平均）
気付いたのは以下の2点。どの桁もバラツキは同じはずなのに、５桁目が明らかに小さいのが不思議。
- １桁目から5桁目へ向かうにつれてバラツキが小さくなる
- 移動平均でみれば、どの桁も「バラツキ幅≒７」ていど
移動平均に関しての私の理解程度はコチラを参照。→ クリック↗