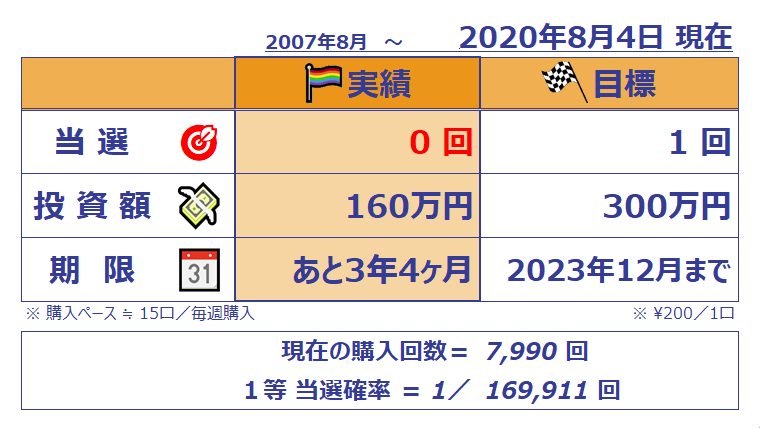
１０８万円赤字。shirono-j🤠です。
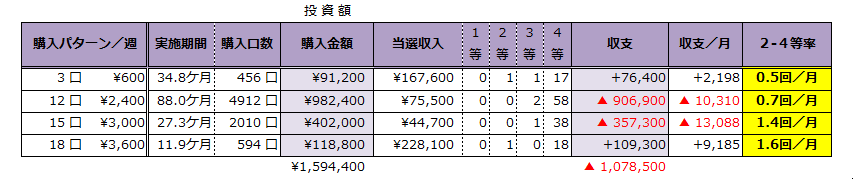
上表は、これまで13年間ミニロトを買い続けた購入方法と、その成績の推移です。
だんだん購入数が増え、それに伴って小当たりも増加しています。（あたりまえですが）
現在は、
ミニロト全31数字中の「18種類の数字」を使い、「18本の予想」を購入する方法で頑張っていますが、まだヒット数が足りません。
１等を獲るには、もっともっとヒット数を増やす必要があります。🤔
ボクの直感力で増やすのはまだ難しいので、物理的に分母を上げて対応します。
要は買う本数を増やします。悲しいですが。😢
買う本数を増やすことは、予想数を増やすことです。
予想数を増やすということは、予想作業フォーマット（EXCEL）の改造が必要。
結構大工事です。
忙しくなりそうだな～。楽しいけど。😅
ミニロト予想
今週も「各桁数字の大きさ」が相応なパターンを主力として予想を組み立てました。
「各桁数字の大きさ」が片寄るパターンが４週連続で出ているので、そろそろ相応になります。（たまにアホほど続くときがありますが）
合わせて、
オレンジパターンを中心にして、ピンクパターンと、前回の１等がふたつかぶってくるパターンがバランスよく派生するように配慮してます。
また、
今週は緑の数字が多かったので、各予想にひとつづつは入れるようにしたかったけど、全部には入れきれませんでした。
上記すべての条件をクリアしようとすると、組み合わせが難しかった。
今週も苦しかったな。
報われてくれ～！😅
ミニロト反省
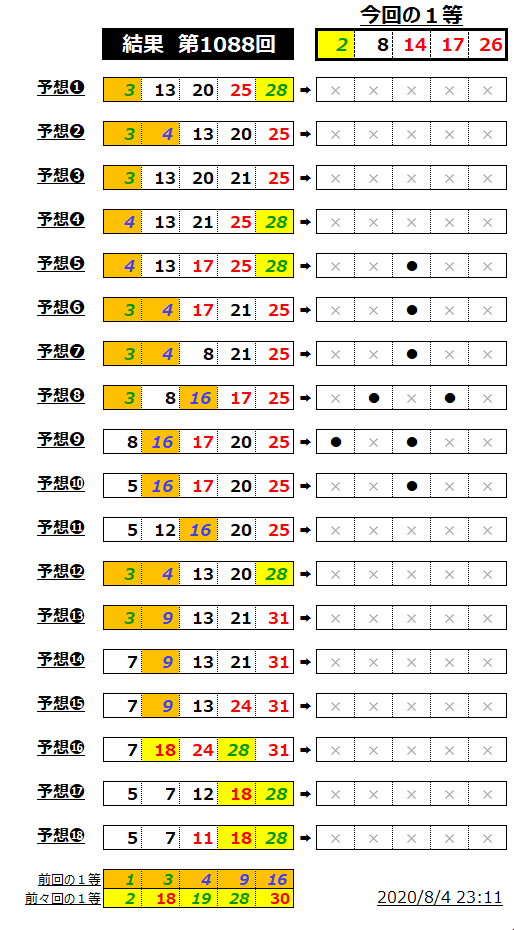
イエローパターンを嫌ったら、イエローパターンがきた。😰
今、「落ち着け、落ち着け」と一生懸命心を静めております。
今週はなんか反省が出ない。
いかん。なんか落ち込んでる。🥀
別にそんなにショックな外れ方じゃないのに。
外れを積み重ねすぎたか？
何をいまさら．．。７千回以上も外しといて。
今日はここまでにしとこう。何かダメだ。
次回までに回復する。🌹
大丈夫！今までも何とかしのいできた。🤠
ミニロト実績
ミニロトチャレンジの源泉となるページ。
目標や考え方、ミニロトの概要なんかを整理してあるんだ。
ぜひ、お立ち寄りください🤠（画像をクリック！）
今週のひと言
田坂さんの講話で聴いたお話。
ボクのミニロトも、
外れても外れても、このまま愚直に考え抜いて予想を続ければ、いつか「当選ナンバー」が見えてしまう、そんな瞬間がきっと来る！💥
直近50回の発生データ
直近50回分のデータを羅列。毎週更新していて、「前回の１等」や「前々回の１等」の出現状況を『色』で表現してある。
※
色の意味に興味のある方はコチラ → 直近２回での出現（色のパターン）
統計データ掲示板
ミニロトのために統計の勉強中。少しでも１等当せんへ近づけないか、何とか攻略できないものかと必死にやってる。
勉強した知恵を利用して整理した、最新のデータをここに公開。アホかと思われるかもですが、勝てば官軍。正義が勝つのではなく、勝った者が正義なのだ！
がんばって、最後に勝つ！🤠
度数分布表；全31数字×桁別
全31数字の発生頻度を「桁別」でカウントして整理した集計表。
「計」と「発生率」の列では、
- 平均以上値＝ピンク枠で太字
- 最大値＝青枠で太字
- 最小値＝緑枠で細字
- その他＝白枠で細字
となっている。
出現度数；ヒストグラム
出目頻度のヒストグラム（度数分布）を「桁別」で書き出したもの。
※
ピンクの部分が「桁ごと」の度数を表し、グレーの部分は全体を表わす。
第１回から現在までの「全抽せんデータ」で分析してグラフ化した。右側の図は 最近勉強した「箱ひげ図」。
度数分布に関しての理解程度はコチラを参照。→ クリック↗
気付いた点としては、
- 桁別なら正規分布に近い
- ５桁目はバラツキが小さい
移動平均と合わせ見ても５桁目はバラツキが小さ目だ。理論的には１桁目と同じはずなんだけどなぁ。よく解らんけどせっかくだから予想へ利用している。
移動平均；折れグラフ
出目頻度の移動平均を「桁別」にとってグラフ化したもの。
過去201回分の移動平均を連続させた 折れ線グラフにしています。
- 最新～ n=8レンジ（８回移動平均）
- 最新～ n=17レンジ（17回移動平均）
- 最新～ n=32レンジ（32回移動平均）
の３種類を、ひとつのグラフに重ね合わせている感じです。
移動平均に関しての理解程度はコチラを参照ください。→ クリック↗
気付い点としては、
- １桁目から5桁目へ向かうにつれてバラツキが小さくなる
- 移動平均でみれば、どの桁も「バラツキ幅≒７」ていど
といったところ。どの桁もバラツキは同じはずなのに、５桁目が明らかに小さいのが不思議。
