継続だけは得意！shirono-j🤠です。
問題は、継続したそのあと！
継続中からコンプリートへ、そしてその向こう側へ。
早く行きたいのに。なかなか進めない。
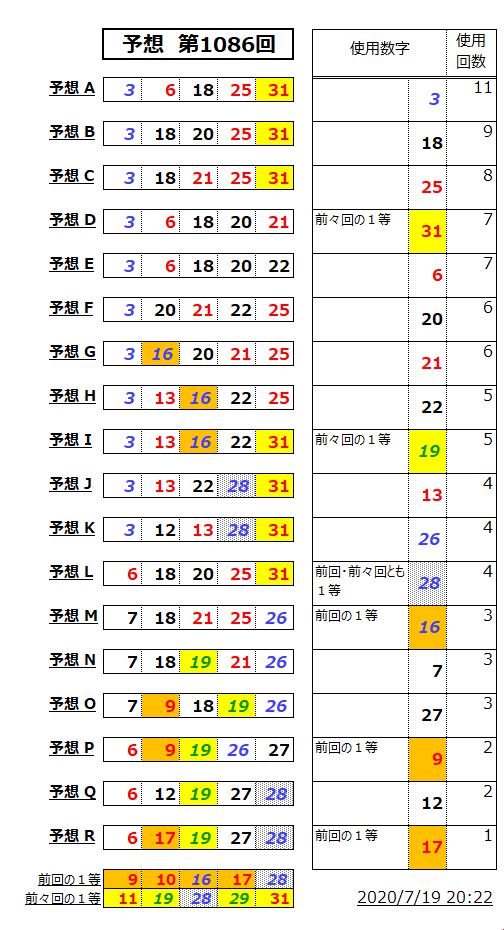
ミニロト予想
スランプかな～。今週は苦しかった。😩
あっ！当たらないという意味じゃなく、予想がなかなかまとまらなかったということで。
外てれるのはいつもの事です。
さて今週は、オレンジパターンの次の回ということで。
オレンジパターンの次の回は特徴が捉えづらくて、非常にヤマが張りにくい。
今週、手掛かりとして意識したのは、
week数の発生パターンは、４週連続で「片寄るパターン」状況なので、今回は「相応になる」パターンへヤマをはりました。
あとは直感で、前々回の１等を多く採用したことかな。
ほんと。今週は気持ちもスランプ。そろそろ当たってくれないとくじけちゃうよ。🤒
来週は切り替えていこう！🤠
参考；予想テータテーブル
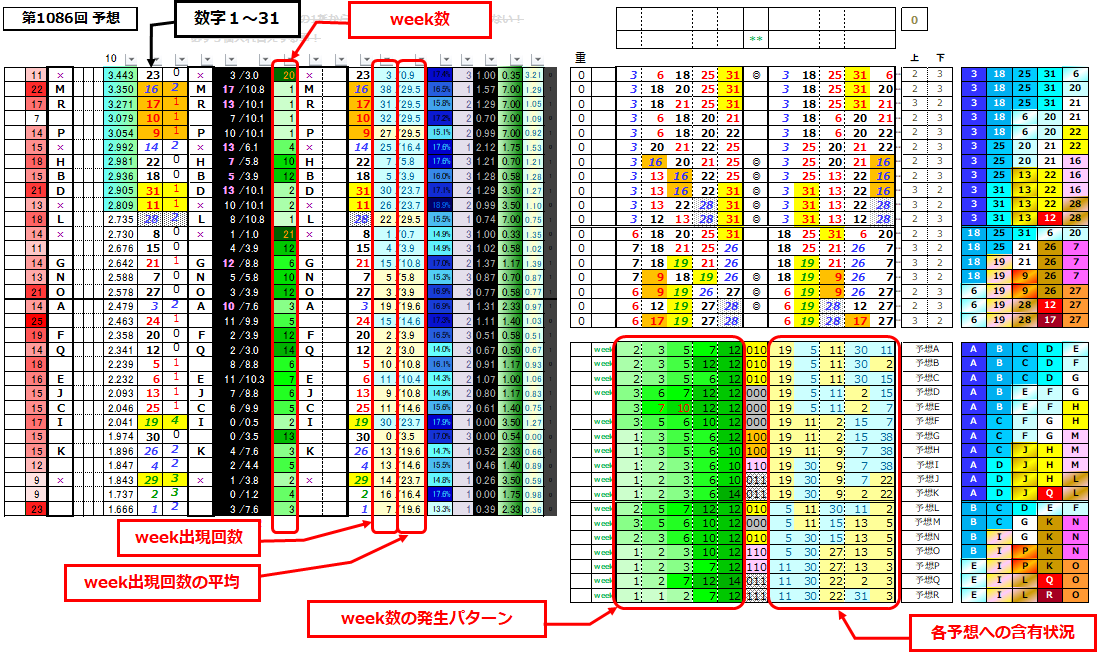
いつも、このデータテーブルで予想してます。🤠
他の人が見てもわかりにくいと思うけど、自己満足で付けました。
今週はかなり苦労したし。３～４時間かかったんちゃうかな。
ミニロト反省
今週の２は、ボクにはちょっと無理。ヒットできない。
②week数の発生パターンが相応になること、
三つの条件が的中したのに、４等すら当たらない。ミニロト恐るべし。
いっいかんっ！闘志が持っていかれそうだ。朽ちる！
なんとか、モチベーションを持ち返さねば！
そうか！今回、一番反省すべきは28の置き所だな。
28は、前回・前々回とも１等のキー数字だったので、欲張って分散した置き方をしていた。
割り切って、下の方へ団子状態にしておけば４等くらいは拾えていた。
26の位置にしておいたら、３ヒットしていたということだ。
ヨシ。今後は、前回・前々回とも１等の数字を使うときは、変に分散したりしない。決めた。
覚えてたらね。🤠
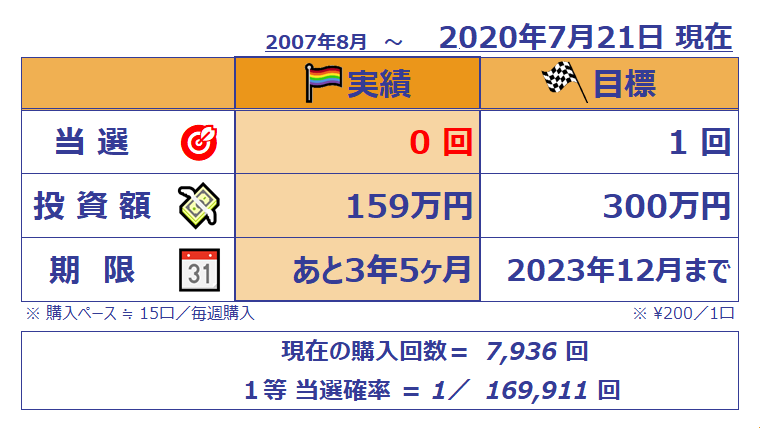
ミニロト実績
ミニロトチャレンジの源泉となるページ。
目標や考え方、ミニロトの概要なんかを整理してあるんだ。
ぜひ、お立ち寄りください🤠（画像をクリック！）
今週のひと言
一本の講話で、３回もツイートしてしまった。
田坂広志さんの講話は、ホントはかなりボリュームのある話をシンプルに分かりやすくされてますね～。
ボク程度でも、感想がスムーズに出せちゃいます。
直近50回の発生データ
直近50回分のデータを羅列。毎週更新して最新を保ちます。
「前回の１等」や「前々回の１等」の出現状況も『色』で表現してある。
※
パターン色について興味のある方はコチラの説明をご覧ください → 直近２回での出現し易さ（色のパターン）
統計データ掲示板
ミニロトのために統計の勉強中。少しでも１等当せんへ近づけないか、何とか攻略できないものかと必死です。
勉強した知恵を利用して整理した、最新のデータをここに公開。アホかと思われるかもですが、勝てば官軍。正義が勝つのではなく、勝った者が正義なのだ！
がんばって、最後に勝つ！🤠
度数分布表；全31数字×桁別
全31数字の発生頻度を「桁別」でカウントして整理した集計表。
「計」と「発生率」の列では、
- 平均以上値＝ピンク枠で太字
- 最大値＝青枠で太字
- 最小値＝緑枠で細字
- その他＝白枠で細字
となってます。
出現度数；ヒストグラム
出目頻度のヒストグラム（度数分布）を「桁別」で書き出したもの。
※
ピンクの部分が「桁ごと」の度数を表し、グレーの部分は全体を表します。
第１回から現在までの「全抽せんデータ」で分析しています。
度数分布に関してのボク🧐の理解程度はコチラを参照ください。→ クリック↗
右側の図は、最近勉強した「箱ひげ図」です。
ボク🤠が気付い点としては、
- 桁別なら正規分布に近い
- ５桁目はバラツキが小さい
移動平均と合わせ見ても５桁目はバラツキが小さ目だ。理論的には１桁目と同じはずなんだけどなぁ。よく解らんけどせっかくだから予想へ利用している。
移動平均；折れグラフ
出目頻度の移動平均を「桁別」にとってグラフ化したもの。
過去201回分の移動平均を連続させた 折れ線グラフにしています。
- 最新～ n=8レンジ（８回移動平均）
- 最新～ n=17レンジ（17回移動平均）
- 最新～ n=32レンジ（32回移動平均）
の３種類を、ひとつのグラフに重ね合わせている感じです。
移動平均に関してのボク🧐の理解程度はコチラを参照ください。→ クリック↗
ボク🤠が気付い点としては、
- １桁目から5桁目へ向かうにつれてバラツキが小さくなる
- 移動平均でみれば、どの桁も「バラツキ幅≒７」ていど
といったところ。どの桁もバラツキは同じはずなのに、５桁目が明らかに小さいのが不思議。
