外し職人。shirono-j🤠です。
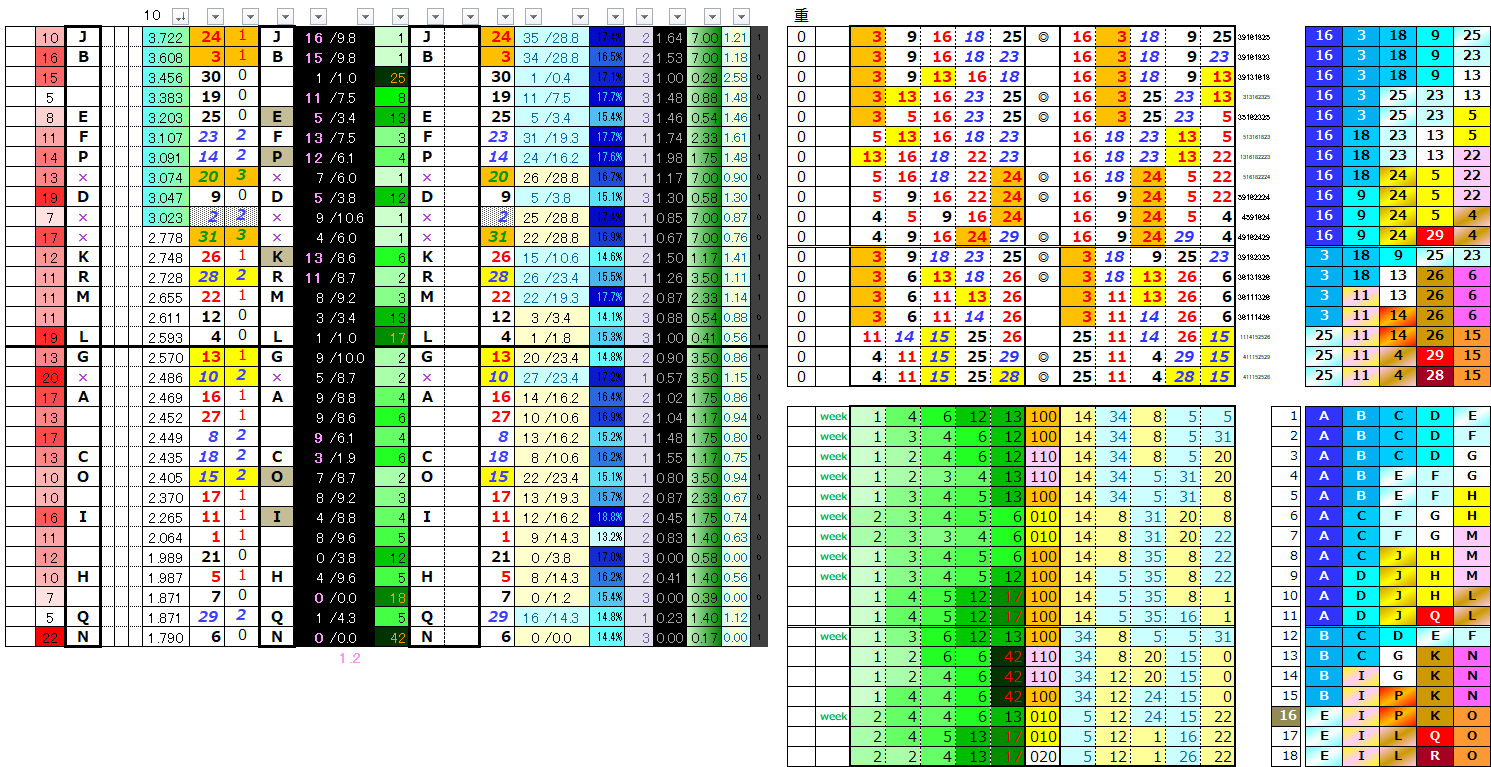
予想作業用のデータテーブルにひと工夫を加えたので、画像で記録してみました。
そのうちに 用語説明ページ⮭ で説明することがあるかもだけど、無理やりいろいろ詰め込んでいるから分かりにくいだろうな～。
まあ、今は誰も見ていないからいいか。😅
ミニロト購入
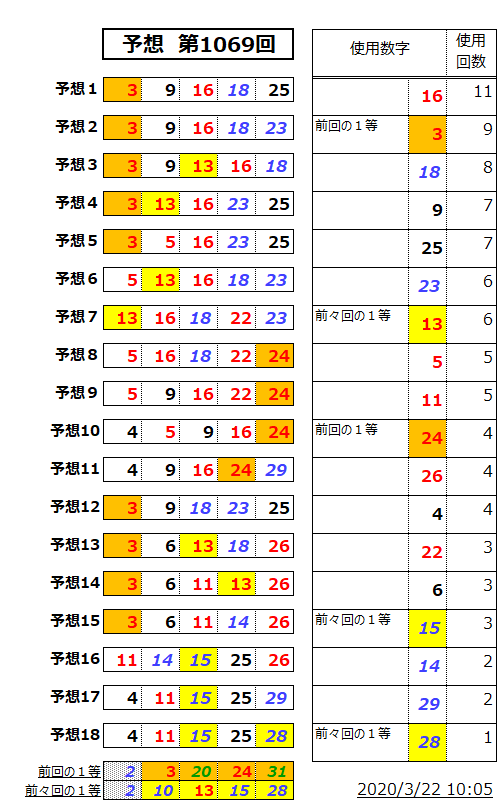
今週は、「前々回の１等」がひとつだけ入るパターンの一点へ絞り込んでもよかったのですが止めておきました。
上記を含む４種類のパターンを使って、手広く構えた形にしてます。
また、
今週も「前回・前々回とも１等」の数字が出やすいとの総合データになっているけど、ここ６週間ほどは出ていません。
「前回・前々回とも１等」の数字がしばらく出なくなる前兆ととらえ、２を使うのは自重しました。
ミニロト反省
１は、可能な限り使用しないと決めています。
１を外したのは仕方がない。
３、９、25は、問題なし。いや、むしろかなりいいポジションにつけていた。
14だったな。最大の反省は。
「week出現回数」が「平均」より大きい数字が、当せんNoの中に４個も入ってくるとはね。
このパターンは、ぼくには予想できない。
おまけに１に邪魔されると、どーしようもない。
４等が当たっただけでも感謝。
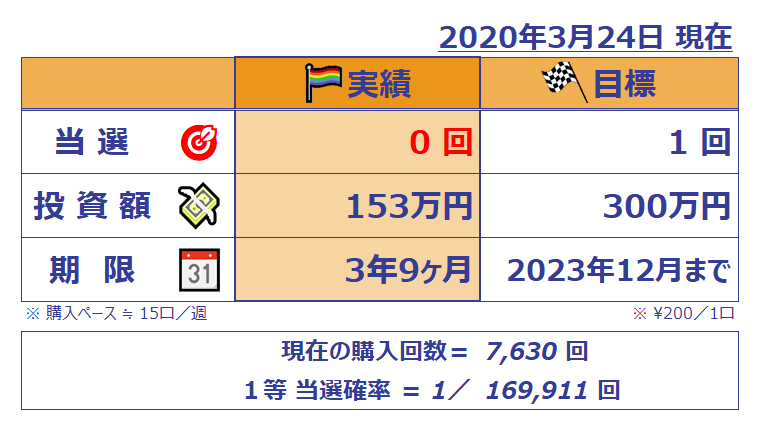
ミニロト実績 2007年8月～
ミニロトチャレンジの源泉となるページ。
目標や考え方、ミニロトの概要なんかを整理してあるんだ。
ぜひ、お立ち寄りください🤠（画像をクリック！）
今週のひと言
ニューズピックスにアカウントを作ってみたんだけど、有料会員ではないので見れない記事があるんですよ。
下の記事、同感です。ぜんぶ読んでみたいな。
ほとんどの人がニュースソースを検証したり、周辺情報を調べたりすることなく、外から当事者に対して石を投げ始めます。
それはほとんど「どれだけうまく石を投げられたか」を競う大喜利のようなもので、これを繰り返していると人間はどんどんバカになる。
SNSの中だけの話ではない。
自分で現場へ見に行かずに、「小手先で調べた情報」で判断する人たちが多くなってきたような気がする。管理職に多い気もする。
なんか間違った方向に行きかけている気がする。
骨のある管理職の人がいないように感じる。
直近50回の発生データ
直近50回分のデータを羅列。毎週更新していて、「前回の１等」や「前々回の１等」の出現状況を『色』で表現してある。
※
色の意味に興味のある方はコチラ → 直近２回での出現（色のパターン）
統計データ掲示板
ミニロトのために統計の勉強中。少しでも１等当せんへ近づけないか、何とか攻略できないものかと必死にやってる。
勉強した知恵を利用して整理した、最新のデータをここに公開。アホかと思われるかもですが、勝てば官軍。正義が勝つのではなく、勝った者が正義なのだ！
がんばって、最後に勝つ！🤠
度数分布表；全31数字×桁別
全31数字の発生頻度を「桁別」でカウントして整理した集計表。
「計」と「発生率」の列では、
- 平均以上値＝ピンク枠で太字
- 最大値＝青枠で太字
- 最小値＝緑枠で細字
- その他＝白枠で細字
となっている。
出現度数；ヒストグラム
出目頻度のヒストグラム（度数分布）を「桁別」で書き出したもの。
※
ピンクの部分が「桁ごと」の度数を表し、グレーの部分は全体を表わす。
第１回から現在までの「全抽せんデータ」で分析してグラフ化した。右側の図は 最近勉強した「箱ひげ図」。
度数分布に関しての理解程度はコチラを参照。→ クリック↗
気付いた点としては、
- 桁別なら正規分布に近い
- ５桁目はバラツキが小さい
移動平均と合わせ見ても５桁目はバラツキが小さ目だ。理論的には１桁目と同じはずなんだけどなぁ。よく解らんけどせっかくだから予想へ利用している。
移動平均；折れグラフ
出目頻度の移動平均を「桁別」にとってグラフ化したもの。
過去201回分の移動平均を連続させた 折れ線グラフにしています。
- 最新～ n=8レンジ（８回移動平均）
- 最新～ n=17レンジ（17回移動平均）
- 最新～ n=32レンジ（32回移動平均）
の３種類を、ひとつのグラフに重ね合わせている感じです。
移動平均に関しての理解程度はコチラを参照ください。→ クリック↗
気付い点としては、
- １桁目から5桁目へ向かうにつれてバラツキが小さくなる
- 移動平均でみれば、どの桁も「バラツキ幅≒７」ていど
といったところ。どの桁もバラツキは同じはずなのに、５桁目が明らかに小さいのが不思議。
