「統計検定4級」に合格😄できたので次は『統計検定3級』を勉強する。
動機は不純で、少しでも「ミニロト予想」に役立てばとの想いから。実際に4級で得た知識は、 ミニロトへも役立てることが出来た。自分は検査部門だから、会社の業務でも役立った。『統計検定3級』はもっと活躍してくれるはずだ。
まずは独学!4級でさえ まあまあ苦労したので正直3級は着いていけるか心配だけど、まだ通信講座は必要ないでしょう、たぶん。
このページはノート替わりの「勉強ページ」だ。はじめは、日本統計学会の公式認定問題集を使って勉強した要点を整理していく。
勉強方法=過去問で独学
4級を合格した勉強方法を繰り返す。
「公式問題集を、標準テキストで調べながら解く」
まずは、これをやってみる。
他にも参考書が必要なら買いたいけれどまずはこの2冊。もしこれでダメだったら通信講座を検討する。調べた感じだと、3級程度では需要がないのだろう講座などはあまり無さそうだ。ここまでは出来るだけ独学でクリアしたい。
教科書と問題集
③日本統計学会認定の標準テキスト

④日本統計学会認定の公式問題集

なるほど統計学園
4級の教科書「データの活用」で紹介してあったサイト「なるほど統計学園」。きっと、3級の学習にも役立つだろう。調べ物は、優先して このサイトで調べることにしたい。ただし、サイト内検索機能がないから少し大変そう。
勉強ノート
このページをノート替わり使う。
各年の問題ごとに、調べなきゃわからなかったことや、勉強しなきゃ知れなかったことを書き留めるのだ。そして、好きなように、つまみ食いのように、わがままに脱線しながら勉強する。落ちても時間がかかっても自分の責任です。
変数形態を事例で理解する
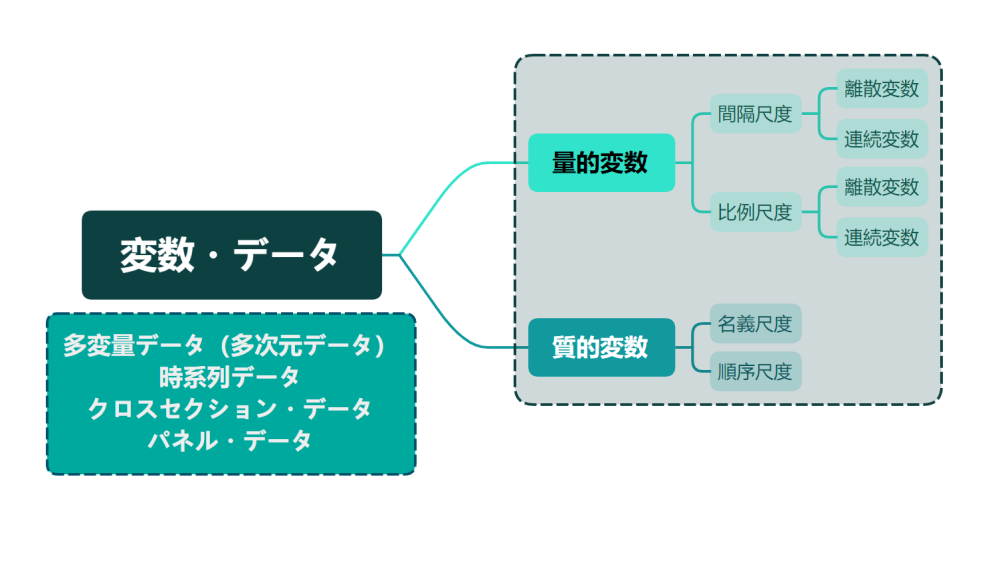
データの種類を覚えるのも、さすがに4級の時よりややこしい。尺度や、離散変数と連続変数の解釈がなかなか厄介だ。使用する場面での、その時々の使い方によっても変化すると理解した。
明確に「小数点があり得ないデータ」、例えばテストの点数やサイコロの目は離散変数でしかあり得ないが、時間や時刻、体重や身長は細かく分ければいくらでも間の数値が存在する。例えば身長169cmと170cmの間には、μm単位でみれば1万種類数値があるし、もっと細かくすることもできる。この場合は連続変数だろう。だけど、使う場面によって「1cm」単位で記録した場合は離散変数として扱うんだろうね。
まぁいい。こんな時は「丸暗記」に限る。事例を表に整理しての理解を試みよう。ネットで調べて事例をかき集た。3級の試験向けには以下のように覚える。
| 性質 | 尺度 | 性質 | 事例 | 覚え(私見) | |
| 量的変数
※ |
間隔尺度 | 順序だけでなく、間隔や距離が解る数字
※ |
離散変数 | 西暦、日付、年齢、知能指数、点数、サイコロの目、ミニロトの数字、その他のロトの数字、日数、人数 | 筆者は、順序尺度のデータを間隔尺度として取り扱うことが多い |
| 連続変数 | 摂氏温度、華氏温度、ゲージ圧力、時刻、 | ||||
| 比例尺度 | 間隔尺度に比例するという性質が加わったもの
※ |
離散変数 | 給料、値段 | ||
| 連続変数 | 絶対温度、絶対圧力、時間数(日数や年数も)、速度、寸法、身長、重さ、血圧、圧力 | ||||
| 質的変数
※ |
名義尺度 | 順序も大小も解らないデータ | 性別、血液型、郵便番号、住所、本籍地、所属学部、学籍番号、電話番号、合否、名前、部署、有無し | 筆者は、番号類を順序があるかのごとく取り扱うことが多い | |
| 順序尺度 | 方向性を持った、順序しかわからないデータ | 順位、満足度、等級、階級、ステージ、順番、ロット番号、グレード、学年、時間帯 | 筆者は、数字の体を取っていれば量的変数であるかのごとく取り扱うことが多い | ||
自分なりの解釈で事例表に整理したが間違っているかもしれない。試験で間違ったら仕方ないと潔く諦める覚悟だ。表を作るにあたり、参考にさせてもらったサイトを記録しておこう。いろいろ沢山のサイトを見たけど、この二つが すごく解りやすかった。
- 学校保健研究;P40 第1回データの要約より
→ 2025/12/7リンクがつながらない=ページが閉鎖されたらしい - サイト;ケムファク「製造データの変数と尺度の種類」より
「サイコロの目」が離散変数であるという情報はネット上に腐るほどあるが、「間隔尺度なのか比例尺度なのか」については誰も何も言わない。
統計学会の資料には ❝量的変数には離散変数と連続変数という分類もある❞ とあるので量的変数であることはたぶん間違いなかろう。(2020年版 統計検定3級対応 データの分析3ページより)
どこにも情報がないので、自分なりの判断として『サイコロの目は、間隔尺度の離散変数』と定義した。
苦手克服! 総和記号「Σ シグマ」
平均値くらいは解っている。
けれど学生のころから苦手を放置していた「∑」が現れ始めた。この後の勉強でガシガシ出てきそうな気がするので今のうちに復習しよう。
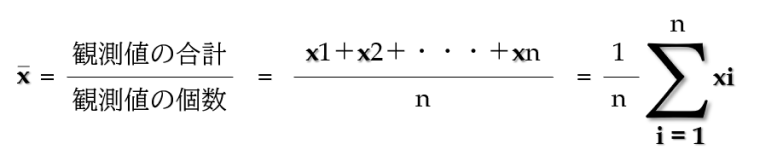
平均値(エックスバー)を表すシグマ記号で押さえておこう。まぁ、だいたい覚えてるんだけど、「i=1」ってのが良く解らないから調べると、
「i」は「スタートの値」で、1づつしか増えない
ということだった。たしか、学生の頃に教わってた。教わってなかったのは、「i」って呼んだり「k」って呼んだりされていること。注意が必要だ。
この三つの記事が すごく解りやすかった。
たぶんキモ!分散、標準偏差
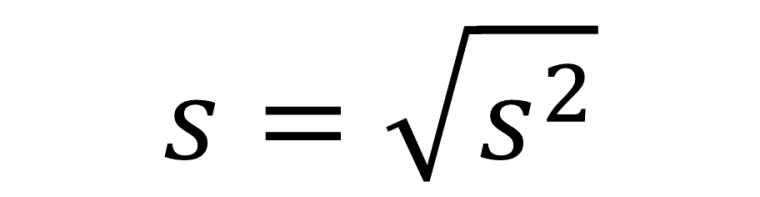
標準偏差=Sについては、今でも体感的な理解は進んでいる。仕事で使ってるから。でも「分散」や「平均偏差」は、理屈は知っていても実際に使った事がないので体感的な理解はできていない。良い機会なので少しだけ突っ込んで調べてみた。きっと3級取得のうえで、最もキモとなる部分であることは間違いないだろう。流行りの AIにも聞いてみた。
■分散について
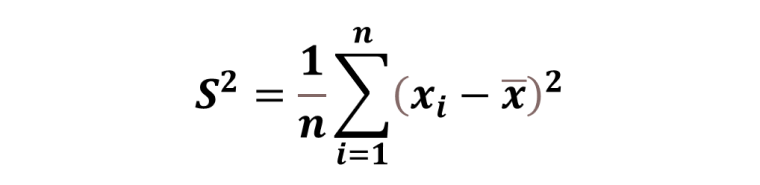

現実で実際に使用されている製品品質管理の事例を1つ教えてください。
ある自動車メーカーが、生産された車の品質を管理するために分散を使用しています。
製造ラインから出荷された車両の一部をサンプリングし、ブレーキシステムの性能をテストします。ブレーキシステムの性能には、摩擦係数や制動距離などが含まれます。
これらのテスト結果から、ブレーキシステムの性能に関するデータの分散を計算し、品質管理の指標として使用しています。
例えば、ブレーキシステムの性能に関するデータの分散が大きい場合は、製造ライン上で何らかの問題がある可能性があり、改善が必要であると判断されます。
一方、分散が小さい場合は、製造ラインの品質管理が優れており、品質の一定性が高いと判断されます。
■平均偏差について
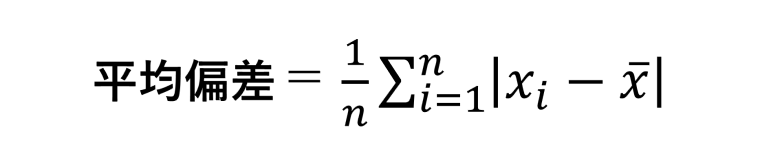
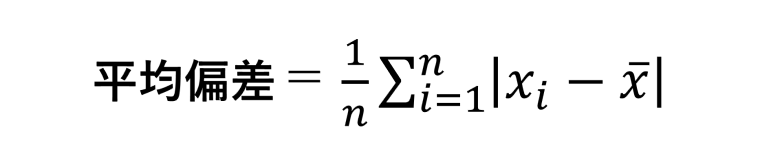



現実で実際に使用されている製品品質管理の事例を1つ教えてください。
ある工場で製造された製品の重さについて、平均偏差を用いて品質管理を行うことがあります。
例えば、ある工場で製造された袋詰めの商品について、1つ1つの袋詰めの重さが異なる場合、消費者にとっては不満に感じられる可能性があります。そこで、製品の品質を一定に保つために、製品の重さについて平均偏差を計算し、製造ラインでの調整や品質管理を行うことがあります。
具体的には、ある時間帯に製造された袋詰め商品の重さを測定し、その平均値から各袋詰めの重さを引いた差の平均を求めます。この平均偏差が大きい場合、製造ラインでの調整や品質管理を見直す必要があると考えられます。
平均偏差が小さいほど、製品の品質が一定していると考えられます。
■分散と平均偏差の使い分けについて



平均偏差と分散を比べた時、分散の方がバラツキの分析に適しているのでしょうか?
平均偏差は、各データの平均値からの差を絶対値で求め、その平均値をとったものです。一方、分散は、各データの平均値からの差を2乗したものを求め、その平均値をとったものです。
分散は、平均偏差よりもバラツキの分析に適しているとされています。なぜなら、平均偏差は絶対値を使っているため、正負の符号が消えてしまい、データのばらつきが過小評価される可能性があるからです。
一方、分散は2乗を使っているため、データのばらつきが過大評価される可能性がありますが、その点を考慮すれば、分散の方がバラツキの分析に適していると言えます。
■分散と標準偏差の使い分けについて



分散を使うべきか、標準偏差を使うべきかは、どのように判断するのでしょうか?
分散と標準偏差は、両方ともデータのばらつきを表す指標であり、どちらを使うべきかは分析目的やデータの性質によって異なります。
一般的に、分散はデータの散らばり具合を定量的に評価するのに有効な指標です。分散は、データの平均値からの差の二乗の平均であり、ばらつきが大きいデータに対しても強い影響を与えます。ただし、分散は平方の単位を持つため、直感的な理解が難しく、また、外れ値がある場合にはその影響を受けやすいという欠点があります。
一方、標準偏差は分散の平方根であり、分散と同様にデータのばらつきを表す指標です。標準偏差は、分散に比べて直感的に理解しやすく、また、外れ値の影響を受けにくいという利点があります。そのため、分布の形状や外れ値の有無に関わらず、データのばらつきを評価する場合には、標準偏差を使用することが多いです。
ただし、どちらの指標を使う場合でも、その結果を適切に解釈することが重要です。分析目的やデータの性質に応じて、適切な指標を選択し、結果を正しく解釈することが重要です。
つまり、『おとなしく標準偏差つかっとけや!』と、チャットGPTさまはおっしゃっている。
ちなみに、標準偏差を表す記号が「s」だったり「σ」だったりするのは、
- 「s」のときは標本の標準偏差
- 「σ」は母集団の標準偏差
の意味となるそうだ。気を付けておこう。
Zスコア(Z値)
Zスコア=(観測値-平均値)÷標準偏差「データを標準化する」とか「標準化された値」「変数を標準化する」など、初めて聞く用語が出てきた。「Zスコア」だ。実務でもけっこう使えそうな気がする。
筆者が学生の時はこんな言葉なかったと思う。ミニロト予想に使えるかは、このあとの「変動係数」のところで考える。現時点では、意味として下記の解釈をした。
平均値からどれくらい離れているかを「同じ倍率で比較」する為の手法
- 解りやすかった記事 → アンケート結果のZスコアを「数学を使わずエクセルで」出す
偏差値の意味
偏差値の計算式が、
((得点-平均点)÷標準偏差)×10+50であることは、いたる所に情報がある。
式の中にある「×10」について、その意味を調べるのにまあまあ苦労した。要は、「差が小さすぎて比較しづらいから、倍率を上げて解りやすくした」という事だった。
調べてみて、偏差値は算出後の数字自体には あまり意味はなく、比較するための尺度だと理解した。
着目として大事なのは、
各実測値の「平均値との差」が、全実測値の「平均値との差」の平均値に対してどれくらいの倍率か
なんだろう。それが、(得点-平均点)÷標準偏差 なのだ。高校受験生のころ偏差値が50とか60とか言われて、どこか心の中でモヤモヤしていたのがスッキリした。
- すごく解りやすい記事をみつけた →「偏差値を求める式の意味」
対数変換;準備編


今後どうも、「対数変換」というものが頻繁に出てきそうな気がする。対数は、17世紀にネイピアさんという方が苦心して発明したもの。航海術に必要なケタの大きな計算をやさしくするために考案されたそうだ。
これまで(4級のとき)も、チラっとは出てきてた気がする。あえて目をそらしていたが、3級では正面から向き合わざるを得ない。今はまだ先に進めないほどは難しくないが、調べて備えてみた。解りやすかった記事は控えておこう。
- 解りやすかった記事→対数変換とは?
変動係数
変動係数=標準偏差÷平均値前記した「Zスコア」の 逆数的な数字みたいだ。「Zスコア」は各測定値(観測値)に対して算出して観察し、「変動係数」は代表値とバラツキの相関を観察する感じだった。
「ミニロトの予想に使えるかも」と期待して計算してみた結果、
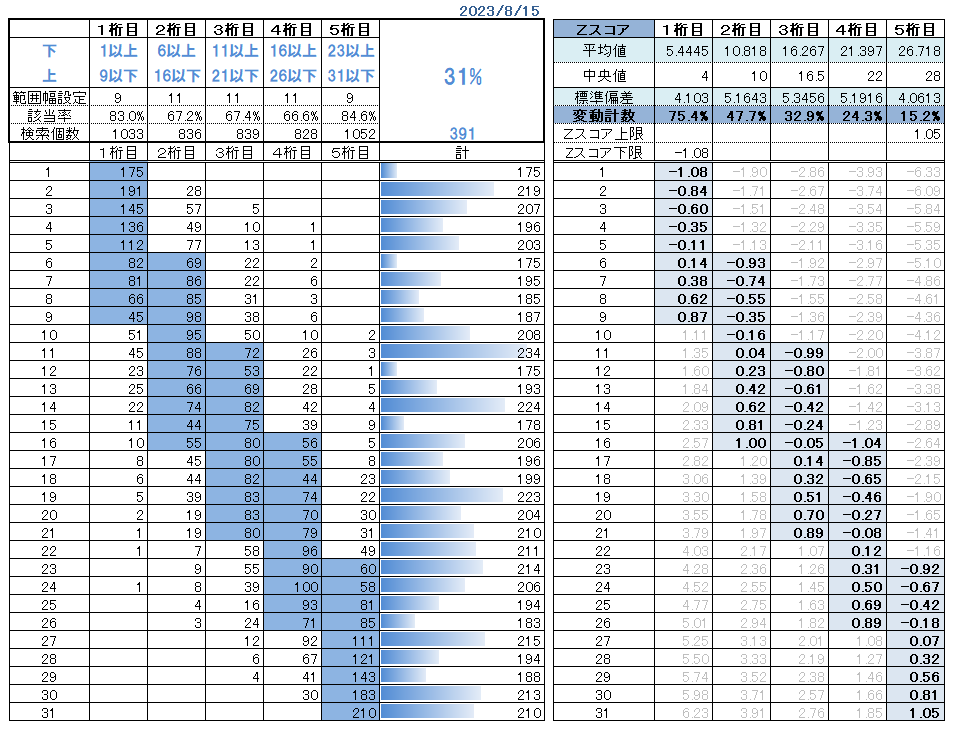
「Zスコア」は、桁-ごとの1等出現パターンを検討するための範囲設定に利用できた。下表のとおり、数字の①と㉛が必ず入るようにZスコアを自動調整するように数式を設定した。これまでたまに「手動で調整」していたものが、今後はたまに「点検するだけ」になるだろう。
「変動係数」は、下表のとおり桁ごとの代表値は大小あるのだが、バラツキには当然ながら法則性がない。変動係数は「平均値が大きくなるとバラツキ値も大きくなる」といった特性のパラメータにしか役立たないようだ。結局、使い方が良く解らなかった。

相関係数
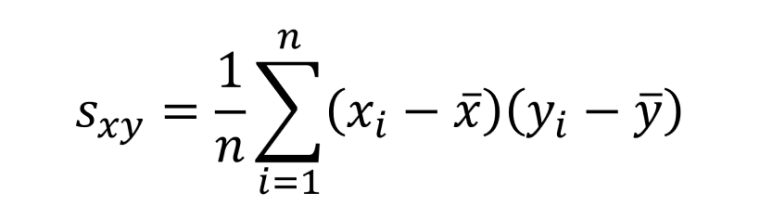
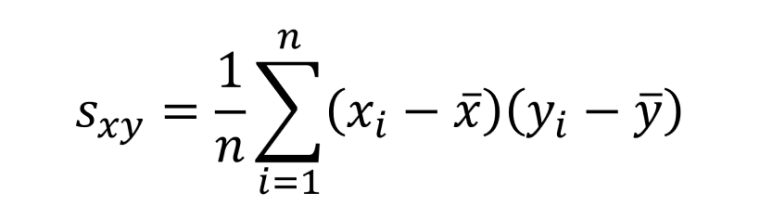
二種類の観測値の関係性をつかむための手法。むかし、訳も解らず使ってた覚えがある。
相関係数の前に「共分散=Sxy」というのがある。名前の通り分散的な役割なんだろう。偏差を二乗する代わりに、ふたつの偏差を掛け合わせて算出される。
「相関係数=r」は、共分散を観測値それぞれの標準偏差で割ったものだ。教本には他にも小難しい理屈や性質、Zスコアとの関係性などが説明されていたが難しくて理解できなかった。難しかったが、以下の理解をした。使えるのは二変数まで。ミニロト予想には役に立ちそうにない。
「-1 から +1」までに算出される計数で、その大小により、
- 相関があるか無いか
- あるなら正比例風の相関か
- または反比例風の相関なのか
を判断する
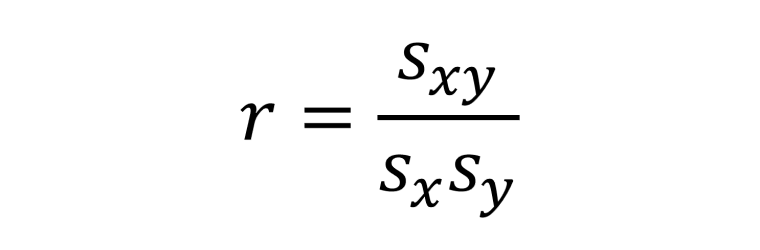
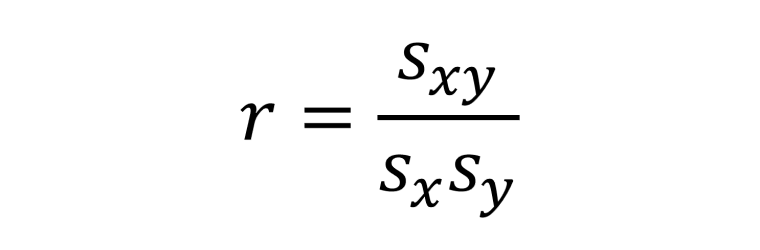
相関係数=(xとyの共分散)÷(xの標準偏差)÷(yの標準偏差)
■「擬相関」に注意!
「擬相関」で検索すると、「疑似相関」でもヒットする。同じ意味で使っても良いと考えられる。相関係数が「1」や「-1」に近くて、計算上では比例や反比例の関係性に見えても、直接は関係ないっていう関係だと理解した。ややこしい。AIに聞いてみたら、googleの「bard」の回答が一番優しかったので記録しておこう。



擬相関とは?
擬相関とは、2つの事象の間に相関が見られるが、因果関係は存在しない状態のこと。両者とも共通の原因の結果である場合などに生じる。
例えば、月ごとのリップクリームの売上と火災の発生件数に強い相関が認められたとして、リップクリームが火災の原因になったり、火災がリップクリーム購入の動機になっているのかというと、そうではなく、「季節による湿度の変動」という共通の原因によって両者に同じ傾向の変動が起こっているだけである。
擬相関の例としては、以下のようなものが挙げられる。
アイスクリームの売上と水の事故
ある小学校の算数の点数と身長の高さ
各国のチョコレートの消費量とノーベル賞の受賞者数
擬相関は、データ分析において注意すべき重要な概念である。相関関係があるからといって、必ずしも因果関係があるとは限らないことを理解しておくことが重要である。
擬相関を回避するためには、以下の点に注意するとよい。
データの収集方法を検討する
データの質を評価する
複数の指標を組み合わせて分析する
統計的な手法を用いて分析する
擬相関を理解しておくことで、データ分析の精度を高め、誤った結論を導くことを防ぐことができる。
変数の変換と分散、共分散、相関係数
(問4.11)
スキージャンプは、飛距離および空中姿勢の美しさを競う競技である。選手は斜面を滑り降り、斜面の端から空中に飛び出す。飛距離Dから得点Xが定まり、空中姿勢から得点Yが決まる。ある大会における58回のジャンプについて考える。
得点Xは、飛距離Dから次の計算式によって算出される。
X=1.80×(D-125)+60.0次の㋐㋑㋒にあてはまる数値を求めよ。
① Xの分散は、Dの分散の㋐倍になる。
② XとYの共分散は、DとYの共分散の㋑倍になる。
③ XとYの相関係数は、DとYの相関係数の㋒倍になる。
テキストの練習問題「問4.11」、これは厳しかった。
テキストの回答を見ると、解答に説明もほぼ無くて公式をダイレクトに使用した直接的な解法しか書いてない。これは「暗記しておかなければ!」と思った。実際の試験に出たら短時間で解かねばならない。暗記してなきゃヤバイ。
そこで、そらで解法を書き出せるようになるまで書き続けた。完全マスターするまで1ヶ月くらい時間をかけた。せっかくなのでここにも書き出しておく。
■公式を構造ごと書き出し
公式の造りを理解。
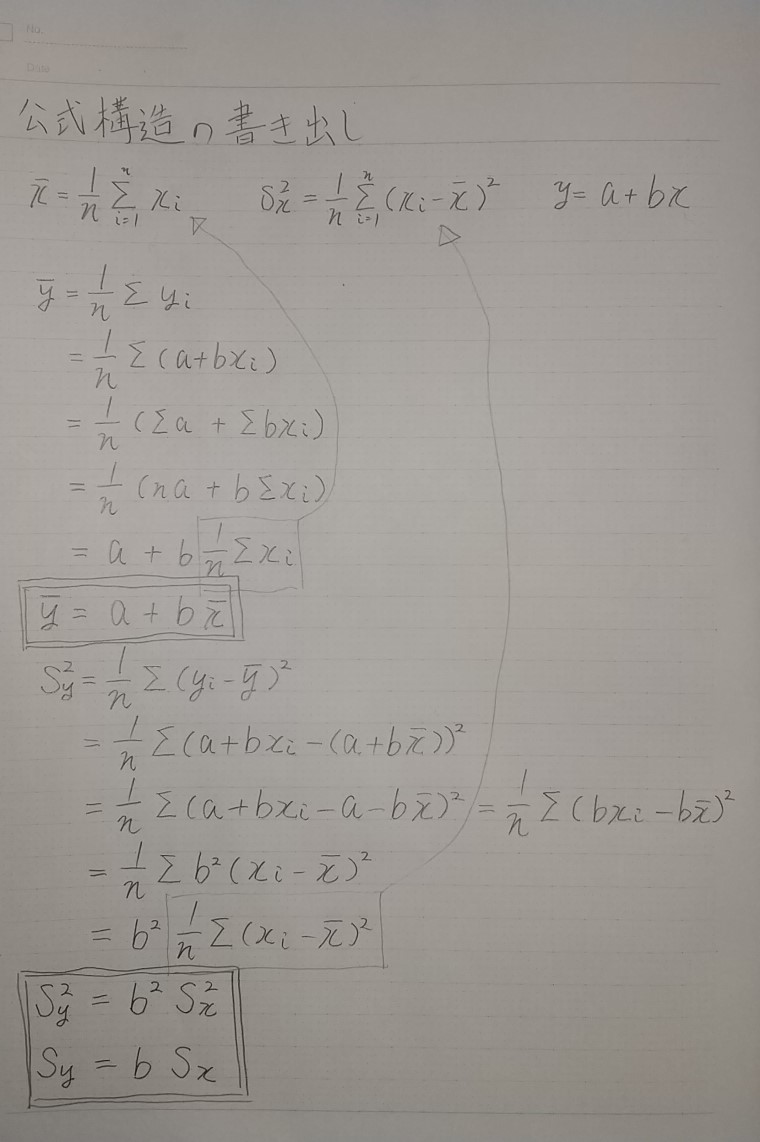
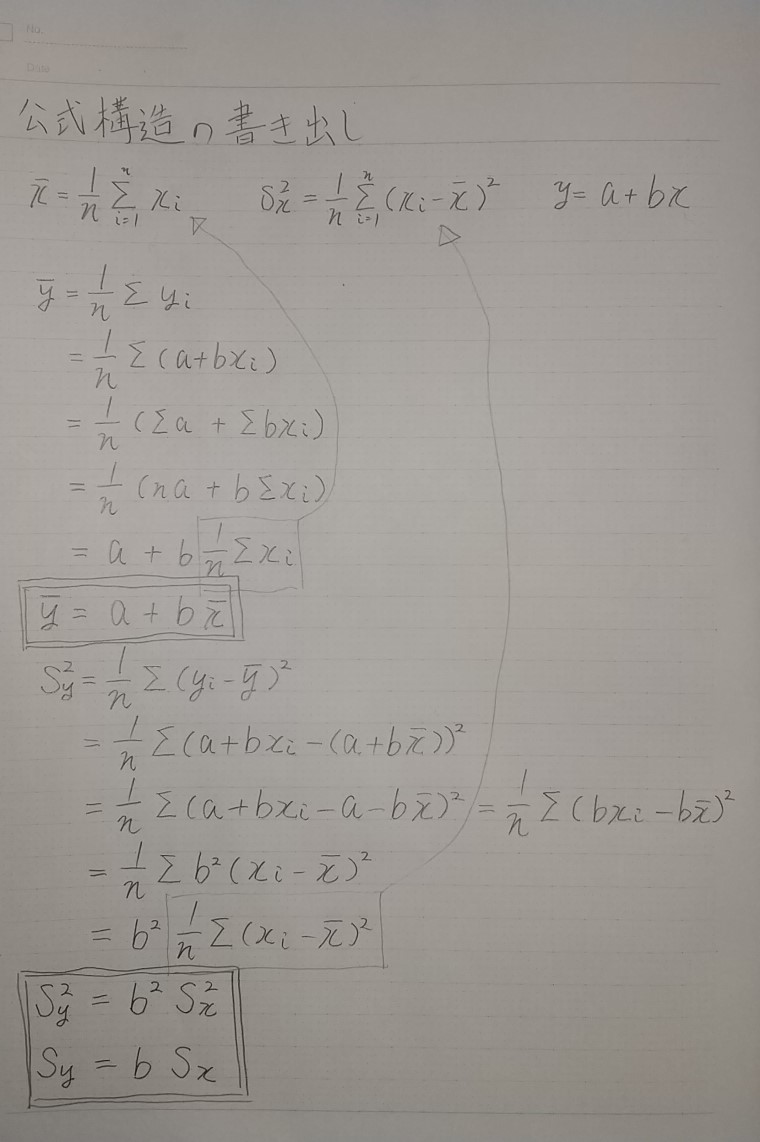
■公式を利用した解答
理解した公式を活用。実際に使っての体得を試みた。


回帰分析
ここは非常に重要で、大きな意味がある部分だと思った。
- 変数xから、変数yを予測することを「回帰分析」という
- 回帰直線y=α+βx の「傾きα」と「切片β」のことを「回帰係数」という
- 回帰直線の回帰係数を予測できる方法のひとつとして「最小二乗法」がある
「二つの変数の関係性を方程式で表すための技術」だ。会社の仕事でも使う場面もあるだろう。ただ、データをあまり重要視していない今の会社ではわかってもらい難い気もする。
それでも、きちんと理解して覚えた方が良いと思った。構造の説明は理解できなかった。ムズいっていうか、ゴチャゴチャしてて非常にめんどくさそうだ。丸暗記にしよう。
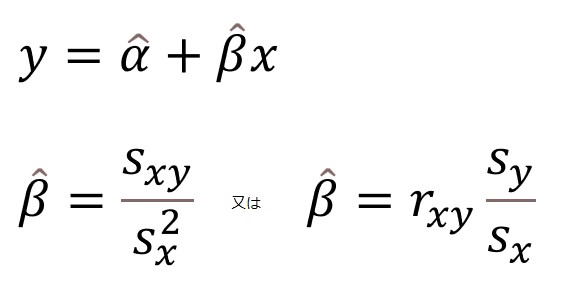
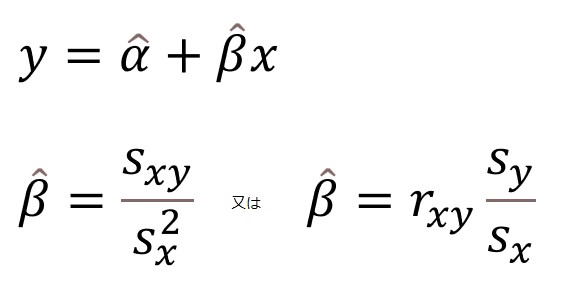
難しすぎる!「平方和の分解」
テキスト内では ❝証明は省略する❞ とあったが、とても大切な事である気がして。他をあたってみたところ解りやすい YouTubeがあったのでこちらで勉強した。
しかし、「回帰分析」にまつわる平方和の分解としては、この後で確認した記事のほうが合っているようだ。残差平方和とか、回帰平方和とかシチュエーションがぴったりだった。→❝平方和の分解と分散分析ができる(重回帰分析)❞
「中間積和項」がゼロになる理屈はどちらも同じ。YouTubeで言うところの「Xi」が、記事で言うところの「Yi」とみればよいはずだ。偏差の平均がゼロになるのは変わらない。
字面的にはこれで理解できたが、感覚として十分に体得出来た気はしない。考え方を応用的に使いこなすのは無理だろう。今はとにかく式の形として暗記してしまう。
下の図を作り、自分なりにかみ砕いて頭へ入れ、あとは書いて書いて、書きまくって丸暗記した。
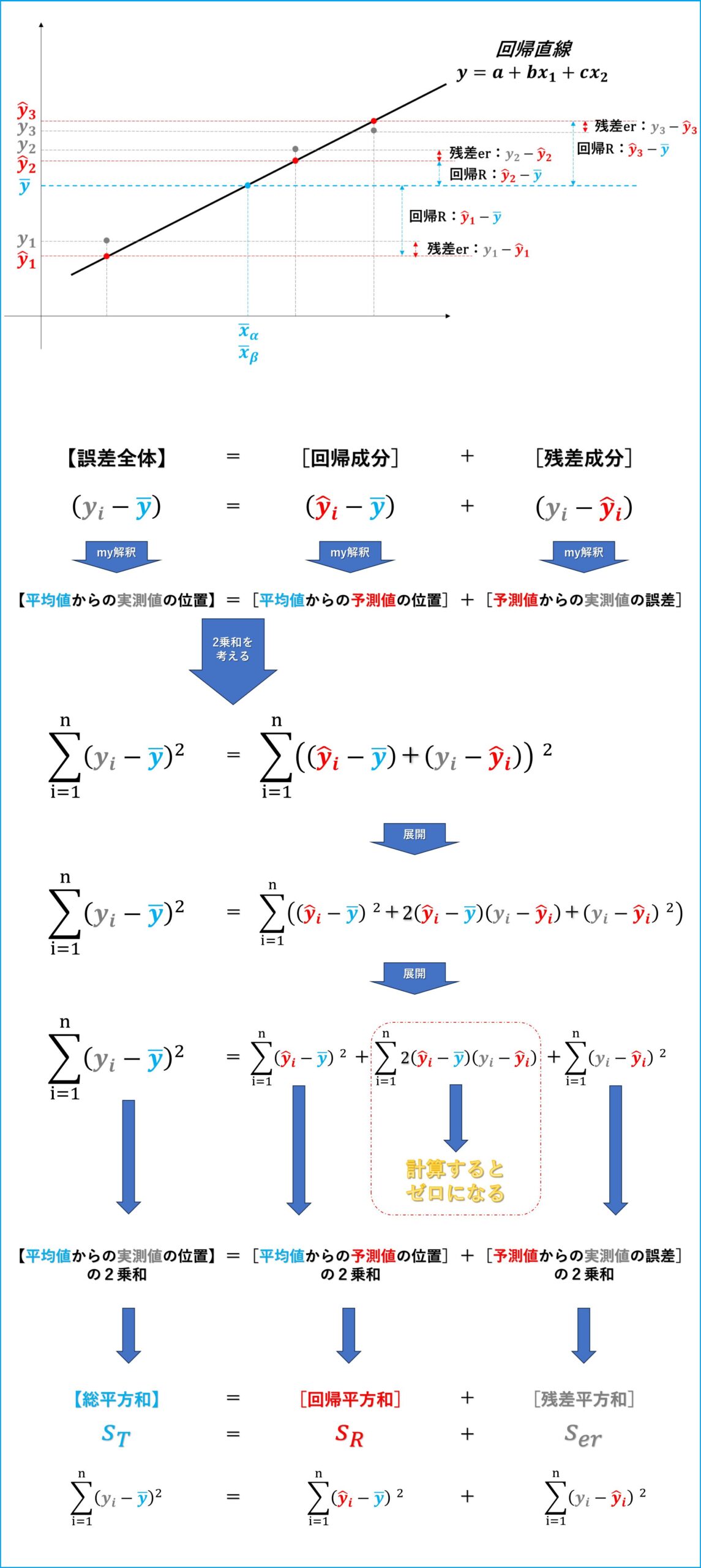

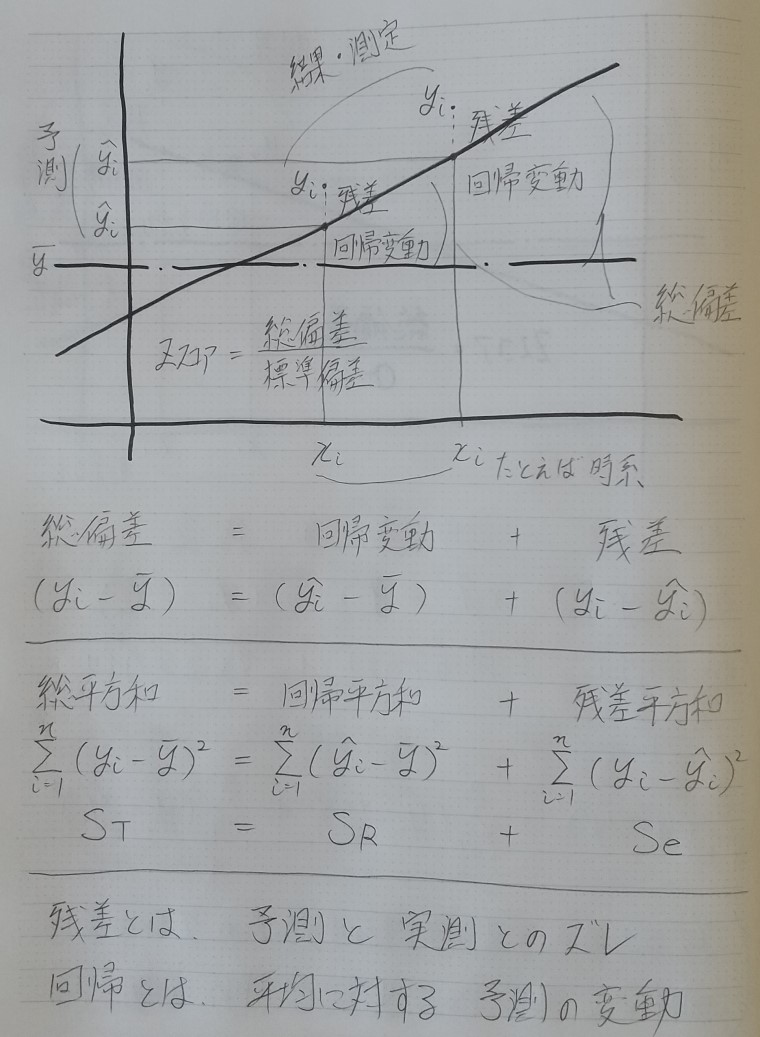

「中間積和項」がゼロになる理屈は理解をあきらめた
上記、計算図内の赤破線枠「計算するとゼロになる」中間積和部分を参考文献で勉強。かなり時間をかけてまったり見たが、「傾き β1、β2の導出」あたりでついていけなくなった。ムリ、あきらめた。
数学記号(集合)
テキストP115「6.確率」ところこから、十分な説明もなく当たり前のように、よくわからん記号をぶっこんできた。なんか見たことはあるが、いきなり「Э」とか「⊃」を使って解説などされてもチンプンカンプンだ。ついて行くためにwebでしらべたら、ベストなブログ記事を見つけた。メチャメチャわかりやすい。助かった。
- このブログ → 受験時点;集合とは?数学記号の読み方や意味、計算問題の解き方
| 記号 | 説明 |
|---|---|
| a ∈ A | a は集合 A の元である |
| a ∉ A | a は集合 A の元ではない |
| A ⊆ B | A は B の部分集合である |
| A ⊂ B | A は B の真部分集合である |
| ϕ | 空集合 |
| A ∪ B | A、B の和集合 |
| A ∩ B | A、B の共通部分 |
いちおう、よくみるやつだけ表に書き出したけど暗記は苦手だ。覚えるのはいったん諦めて先へ進む。
お勉強中!
現在勉強中。他にもやりたいことあるし、とても時間がかかっている。
安心!カンタン?受験の手順
ネットで調べた限りではかなり受験しやすそうで安心だ。
場所や日時は、まず最寄りの会場を自分で選び、選んだ会場で受験日を選べるようだ。(CBT方式試験)いくつか見てみたら、関東から南の地域では だいたい20日/月くらいは試験を受けれる日だった。北日本はあまりやってないみたい。
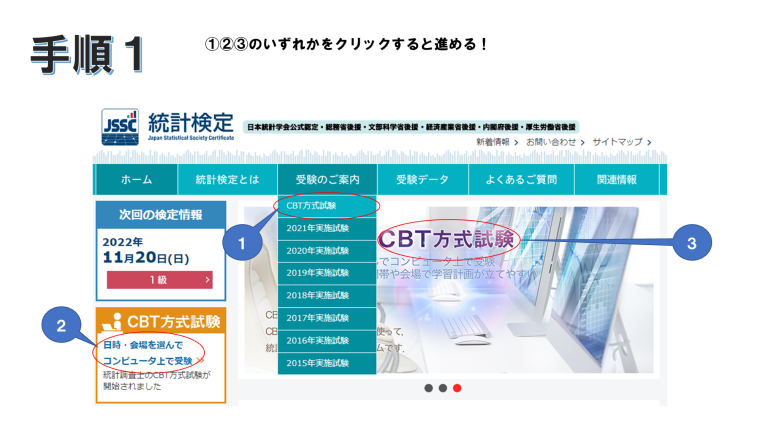



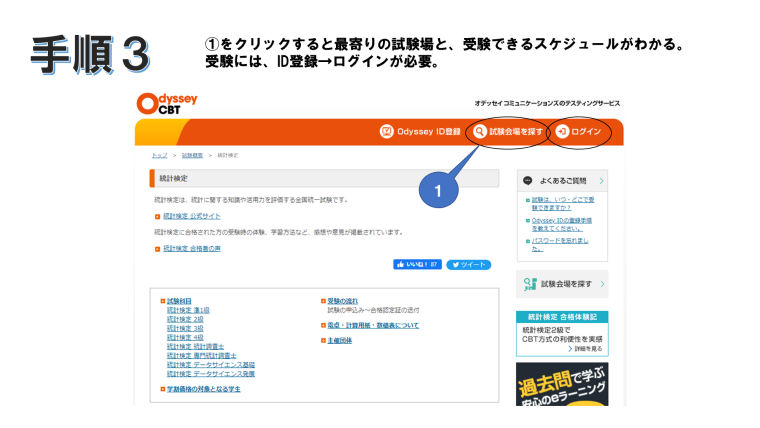

挑戦は続く!
3級に合格したら次は『2級』にチャレンジだが3級合格すら程遠い。ステップアップの手順を以下の記事へ整理しているが、すんなり進める気がしない。